Superfici Equipotenziali

Dettagli

Categoria: Elettrotecnica

Pubblicato Domenica, 07 Aprile 2013 10:25

Scritto da Super User

Visite: 10594

In fig. 1.11 è riportata ancora la carica q, posta nel punto P₀ di un campo uniforme. Spostiamo la carica nel punto P₂, con un movimento perpendicolare al vettore K; il lavoro compiuto dalla forza elettrostatica in questo caso è

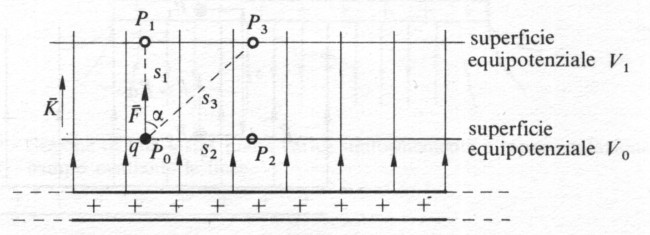
Fig 1.11 - Energia di una carica in un campo elettrico uniforme

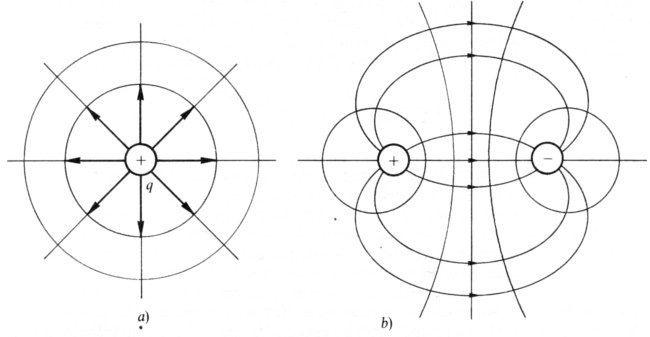
Fig 1.12 - Superfici equipotenziali di campi non uniformi; a) carica puntiforme; superfici equipotenziali sferiche e concentriche; b) coppie di cariche; superfici equipotenziali sferiche, ma non concentriche.

nullo (α = 90°; cos α = 0); l'energia potenziale nel punto P₂ è quindi uguale a quella nel punto P₀, e la differenza di potenziale fra i due punti è nulla.
L’insieme di tutti i punti aventi la stessa energia potenziale costituisce una superficie equipotenziale, che ha la proprietà di essere perpendicolare in ogni punto alle linee di campo.
Nel campo uniforme che stiamo considerando, le superfici equipotenziali sono rappresentate da piani paralleli alla piastra carica; con altre configurazioni di campo le superfici equipotenziali, rimanendo perpendicolari a K in ogni punto, assumono forme più complesse, come negli esempi di fig. 1.12.
Ritornando alla figura 1.11, consideriamo 10 spostamento s₃ che porta la carica da P₀ a P₃, appartenente alla stessa superficie equipotenziale di P₁. il lavoro compiuto dalla forza elettrica vale

essendo

Possiamo ottenere lo stesso risultato scomponendo il percorso della carica in due tratti: si porta dapprima la carica in P₁, compiendo il lavoro L₁; successivamente si porta la carica da P₁ a P₃, senza compiere alcun lavoro: il lavoro totale è ancora pari a L₁.
Si ottiene ancora lo stesso valore del lavoro con il percorso P₀ — P₂ — P₃.

Generalizzando si afferma che il lavoro compiuto nello spostare una carica non dipende in alcun modo dal percorso scelto, ma solamente dalla differenza di energia W₀ — W₁ tra le superfici equipotenziali di partenza e di arrivo.

Un campo che possegga questa proprietà è detto conservativo; un esempio di campo conservativo, oltre a quello elettrostatico, è rappresentato dal campo gravitazionale, con cui il campo elettrico ha strette analogie.
La d.d.p. fra le superfici equipotenziali considerate vale

avendo posto.

I termini V₀ e V₁ rappresentano i potenziali delle rispettive superfici; di essi si conosce la differenza, mentre non è possibile conoscerne i singoli valori assoluti, che, d'altra parte, non sono necessari nello studio dell’elettrotecnica.
Per comodità si assume arbitrariamente una superficie equipotenziale di riferimento, alla quale si attribuisce potenziale uguale a zero. I potenziali delle altre superfici rimangono cosi determinati.
Come superficie di riferimento si assume normalmente la Terra; nei sistemi isolati da terra si assume un conduttore a scelta, che prende il nome di massa.
In un campo uniforme la d.d.p. fra due superfici equipotenziali è data dal prodotto della loro distanza d per il modulo del vettore campo elettrico K

Il modulo di K risulta cosi

A parità di differenza di potenziale il campo risulta tanto più intenso quanto più le superfici sono vicine; la direzione di K è perpendicolare alle superfici equipotenziali, ed il suo verso è diretto dal potenziale maggiore verso quello minore. Poiché la d.d.p. si misura in volt, e la distanza in metri, il campo K si misura in volt/metro, anche se spesso nelle applicazioni pratiche si usa il kV/cm.
In un campo non uniforme, come quello rappresentato in fig. 1.13, il

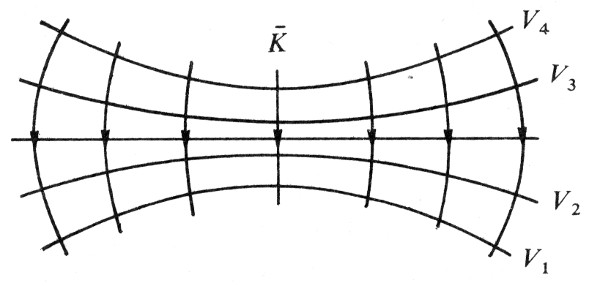
Fig 1.13 - Campo non uniforme

1. Il modulo del vettore campo elettrico K è inversamente proporzionale alla distanza fra le superfici equipotenziali
2.  La densità delle linee di campo, che è proporzionale a K, è maggiore dove la distanza fra le superfici è minore.
3. Le linee di campo e le superfici equipotenziali si intersecano ad angolo retto in ogni punto.

vettore campo risulta più intenso dove la distanza fra le superfici equipotenziali è minore; poiché la densità delle linee è proporzionale al modulo del campo, esse risultano più addensate dove le superfici equipotenziali sono più vicine.

Nel tracciare il grafico ricordiamo ancora una volta che le superfici equipotenziali sono perpendicolari in ogni punto alle linee di campo. 

• < Prec
• Succ >