Forze meccaniche fra correnti

Dettagli

Categoria: Elettrotecnica

Pubblicato Domenica, 06 Ottobre 2013 12:41

Scritto da Super User

Visite: 4042

Si è visto al paragrafo precedente che una corrente è circondata da un campo magnetico; una seconda corrente immersa in tale campo è sottoposta ad una forza meccanica (ci siamo serviti proprio di questo fenomeno per misurare B in ogni punto). Possiamo quindi affermare che due conduttori di lunghezza l, affacciati alla distanza d, percorsi da corrente si scambiano una forza meccanica. Le formule viste finora sono sufficienti per il calcolo di tale forza.

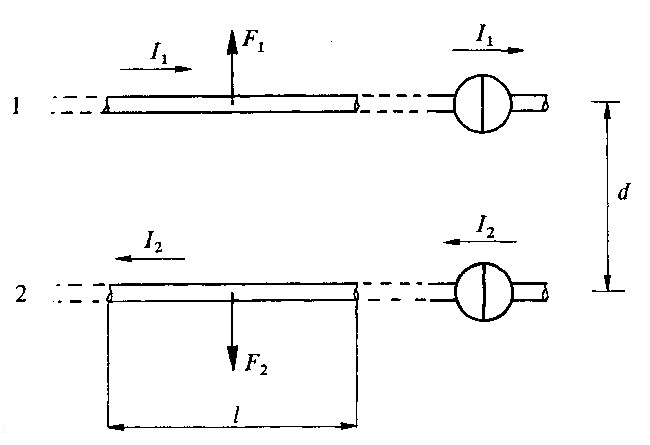
Fig 3.2.9 - Forze meccaniche fra correnti

Nella disposizione circuitale di fig. 3.2.9, valutiamo il modulo del vettore B₁ in corrispondenza del conduttore 2, dovuto alla presenza della corrente I₁ nel conduttore 1

la forza F₂ sarà

<

con lo stesso procedimento si ricava 1a forza F₁

Quando I₁ = I₂ = I la forza diventa

(F in Newton, l e d in metri, I in ampere). Il Valore di senα non compare nella formula, perché con la disposizione di fig. 3.2.9 risulta uguale ad uno (i due conduttori sono paralleli, e quindi l'angolo α fra B ed il conduttore 2 è pari a 90°).

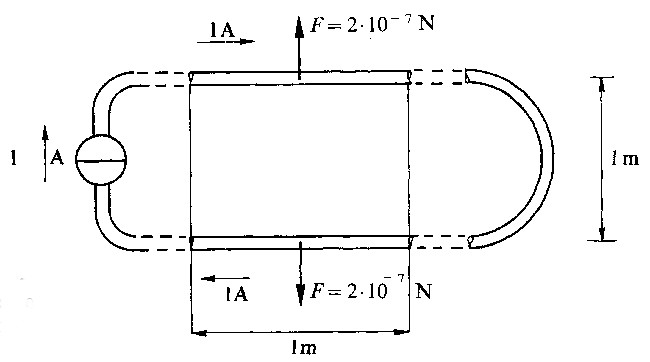
Fig 3.2.10 - Campione fisico dell'Ampere

Se ora adottiamo i valori unitari come in fig. 3.2.10: I₁ = 1 A, I₂ = 1 A, d=1 m, l=1 m, si ricava

Le due forze sono repulsive perché le correnti hanno versi opposti. La disposizione illustrata in fig. 3.2.10 costituisce proprio il campione fisico dell'ampere.

Una corrente ha l’intensità di 1 ampere se, percorrendo due conduttori paralleli distanti 1 m e lunghi 1 m, esercita su ciascuno di essi una forza

• < Prec
• Succ >