Trasformatore monofase ideale

Dettagli: Categoria: Elettrotecnica; Pubblicato Domenica, 21 Settembre 2014 10:42; Scritto da Super User; Visite: 6906

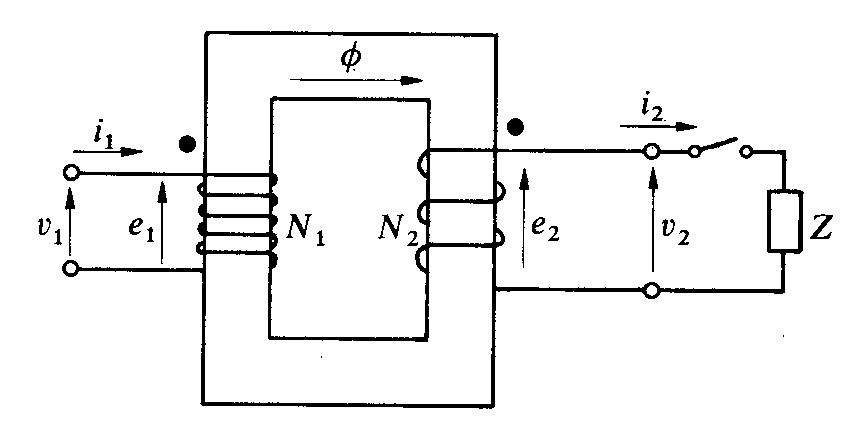
Fig. 1.5 - Schema elettrico di un trasformatore. Convenzioni di segno delle tensioni e delle correnti.

Consideriamo la fig. 1.5 dove due avvolgimenti aventi rispettivamente N₁ e N₂ spire sono avvolti intorno a un nucleo magnetico.

Per semplicità di trattazione e in prima approssimazione consideriamo il trasformatore ideale con le seguenti caratteristiche:

accoppiamento perfetto tra le due bobine: il flusso creato da un avvolgimento si concatena completamente con l'altro;
perdite trascurabili sia nel rame sia nel ferro;
bassa riluttanza del circuito magnetico.

Se si collega un generatore ideale di tensione alternata v₁ Si considera il caso generale di tensione alternata (non necessariamente sinusoidale), cioè periodica, a componente continua nulla in un periodo. all'avvolgimento primario del trasformatore, si realizza il circuito di fig. 1.5. l'interruttore sul secondario Viene lasciato aperto in modo che non circoli alcuna corrente secondaria: in queste condizioni il trasformatore funziona a vuoto.

L'avvolgimento primario costituisce un carico puramente induttivo e assorbe una corrente in detta corrente magnetizzante, la quale produce a sua volta un flusso magnetico Φ(t). Le variazioni nel tempo di Φ(t) sono tali da indurre nell'avvolgimento una tensione e₁, che, in ogni istante, si oppone esattamente alla tensione applicata v₁, in accordo con il 2° principio di Kirchhoff

$\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ e_{1}=v_{1} }}\;\;in\;\; ogni\;\; istante$

Il ﬂusso Φ(t) è generato dalla corrente magnetizzante i_μ, ma è la tensione primaria che ne stabilisce la forma d'onda e il valore.

Per questa ragione, nella trattazione che segue, si deve partire dalla forma d'onda della tensione applicata, ricavare la forma d'onda e il valore del flusso e solamente in ultimo sarà possibile ricavare la corrente magnetizzante i_μ.

Nota la forma d'onda della tensione, si ricava immediatamente quella del flusso necessario a sostenerla, ricordando che

$\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ e_{1}=v_{1} =N_{1}*\frac{d\phi}{dt} }}$

dove dΦ/dt e la tensione indotta in ogni spira.

Da questa espressione ricaviamo la variazione del flusso nel tempo

$\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ d\phi =\frac{1}{N_{1}}*e_{1}dt }}$

Riferendoci alla fig. 1.6 b, che rappresenta la tensione indotta da un flusso variabile nel tempo, osserviamo che il prodotto E₁ *dt corrisponde all'area tratteggiata: possiamo così stabilire la proporzionalità tra la variazione di flusso dφ e l’area E₁ *dt racchiusa sotto il diagramma della tensione

$\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ d\phi =\frac{1}{N_{1}}*E_{1}dt=\frac{1}{N_{1}}*area\;\;tratteggiata }}$

Estendendo il ragionamento all'intervallo di tempo Δt otteniamo che la corrispondente variazione ΔΦ è proporzionale all'intera area racchiusa sotto la semionda rettangolare $\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ \Delta \phi =\frac{1}{N_{1}}*E_{1}\Delta t }}$

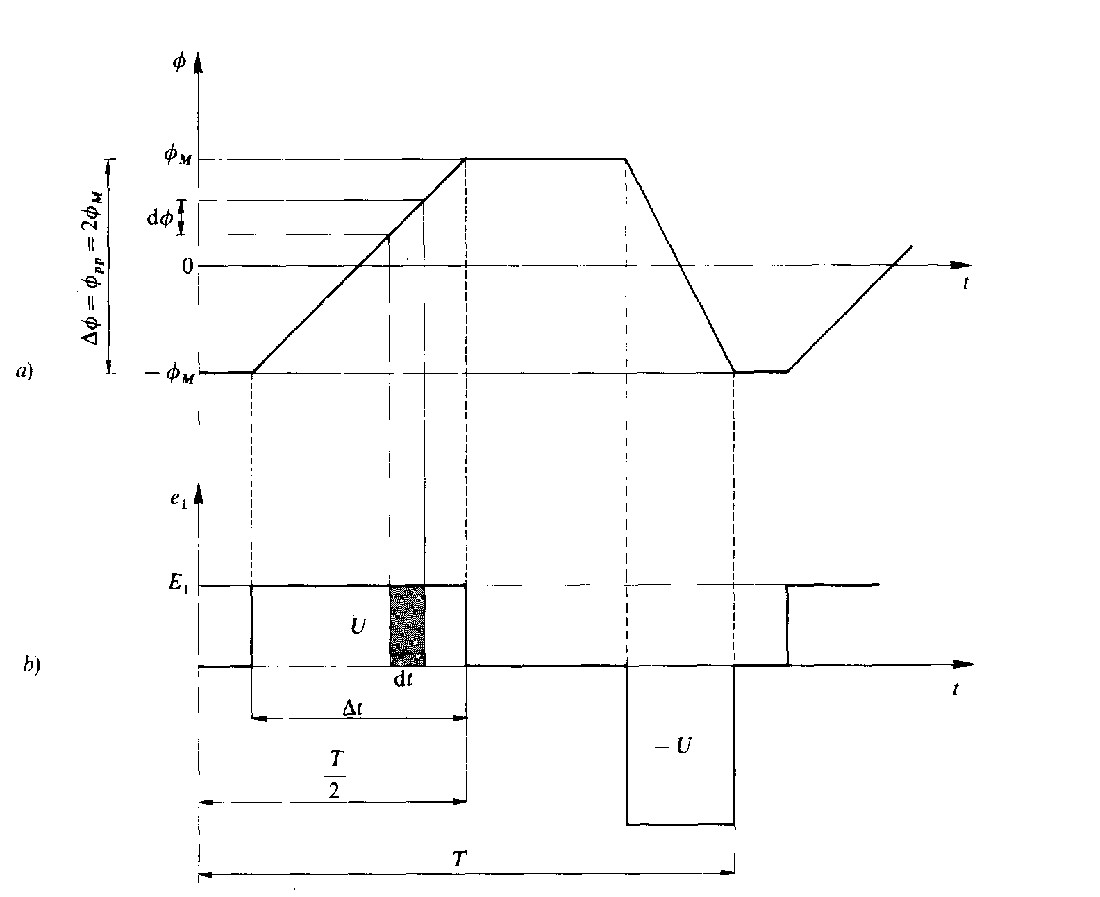
Fig. 1.6 - Relazione tra tensione primaria e flusso. La variazione di flusso Δ Φ è proporzionale all'impulso di tensione.

L’area E₁*Δt è detta impulso di tensione U ed è misurata in V*s (vedi articolo «Tensione indotta come derivata del flusso»); la precedente formula diventa

$\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ \Delta \phi =\frac{1}{N_{1}}*U }}\;\;da\;\;cui\;\; {\color{Red} \mathbf{ U=N_{1}*\Delta \phi =\Delta \phi _{c} }}$

L’impulso di tensione è pari alla variazione del ﬂusso concatenato ΔΦ_c,

Ricordando che il valor medio E_m della tensione in un semiperiodo è pari al valore dell'impulso diviso il semiperiodo stesso, possiamo porre

$\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ E_{m}=\frac{U}{T/2};\;\;\;\;\;\;\;\;\;\;\;\;\;U=E_{m}*\frac{T}{2} }}$

Sostituendo nell'espressione di ΔΦ, si ricava

$\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ \Delta \phi =\frac{1}{N_{1}}*E_{m}*\frac{T}{2} }}$

Vediamo dalla ﬁg. 1.6a che il valore massimo del flusso Φ_M risulta

$\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ \phi _{M} =\frac{\phi _{pp}}{2}=\frac{\Delta \phi}{2} }}$

ricavando così

$\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ \phi _{M} =\frac{1}{2}\Delta \phi =\frac{1}{2}*\frac{1}{N_{1}}*E_{m}*\frac{T}{2}=\frac{E_{m}*T}{4N_{1}} }}$

ed essendo

$\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ T=\frac{1}{f} }}$

scriviamo la formula fondamentale del flusso del trasformatore

$\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ \phi _{M}=\frac{E_{m}}{4N_{1}*f} }}$

Questa relazione è valida per qualsiasi forma d ’onda e stabilisce che il valore massimo del ﬂusso è proporzionale al valore medio della tensione e inversamente proporzionale al numero di spire primarie e alla frequenza.

L'impulso di tensione -U, del semiperiodo negativo, deve avere valore esattamente uguale e opposto all’impulso del semiperiodo positivo, come illustrato in ﬁg. 1.6, dove le aree U e -U sono equivalenti, anche se di forma diversa. In altre parole la tensione primaria deve essere esente da componente continua.

Solo in tal caso la diminuzione del ﬂusso in un semiperiodo compensa esattamente l'aumento del ﬂusso nell’altro.

Se questo bilanciamento non fosse assicurato, il ﬂusso subirebbe un certo incremento in ogni periodo e porterebbe in saturazione il circuito magnetico.

A questo punto possiamo ﬁnalmente determinare la corrente magnetizzante i_u utilizzando la relazione

$\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ i_{\mu}=\frac{\phi*\Re }{N_{1}} }}$

dove ℜ rappresenta la riluttanza del circuito magnetico e, nell'ipotesi semplifìcativa di circuito magnetico lineare, cioè di riluttanza costante,‘ tale corrente h’a'la"stessa forma d’onda del ﬂusso.

In ﬁg. 1.7 è illustrato un esempio nel quale la tensione applicata v₁ ha forma d’onda rettangolare simmetrica. Il ﬂusso dovrà avere andamento nel tempo e valori tali da indurre in ogni istante la tensione e₁ esattamente identica a v₁: esso avrà necessariamente la forma d’onda triangolare di ﬁg. 1.7 b, come possiamo veriﬁcare graﬁcamente.

A partire dall’istante zero il ﬂusso diminuisce con andamento lineare ﬁno all’istante T/4. Poiché la sua pendenza, cioè la sua derivata, è costante e negativa, la tensione sarà costante e, con le convenzioni di segno adottate in fig. 1.5, sarà anche negativa.

Nell'intervallo da T/4 a 3/4 T la pendenza del flusso e costante e positiva (fig. 1.7).

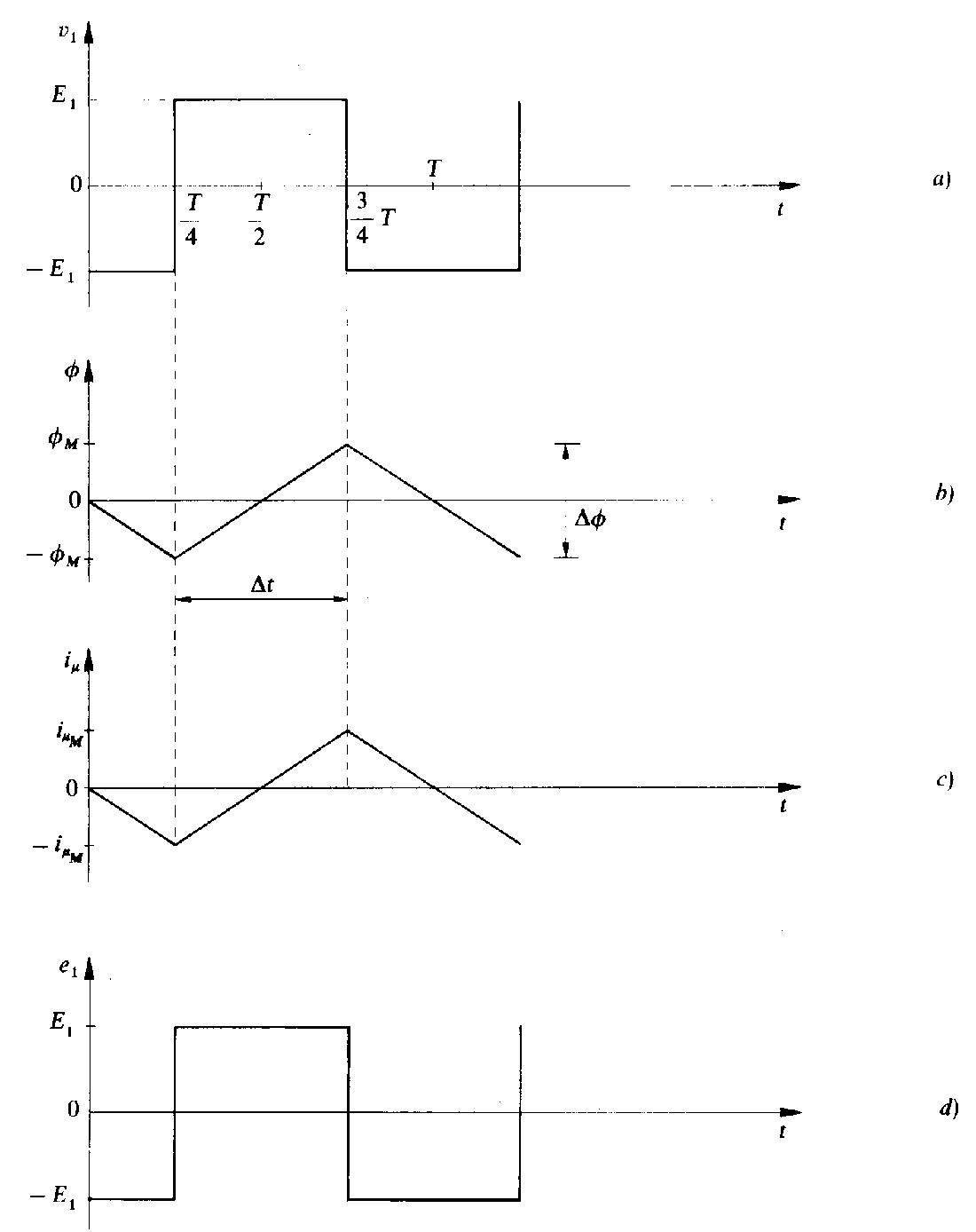
L2fig1.2.7

Fig. 1.7 - Andamento nel tempo delle grandezze primarie: (a) tensione applicata; (b) flusso; (c) corrente magnetizzante; (d) tensione indotta nel primario.

Il valore massimo del flusso viene calcolato a partire dalla formula fondamentale del flusso

$\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ \phi _{M}=\frac{E_{m} }{4N_{1}*f} }}$

Con la forma d'onda di questo esempio vale l'uguaglianza

$\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ E_{m}=E_{1} }}$

e risulta

Avendo ipotizzato l'accoppiamento perfetto tra le due bobine, il flusso concatena completamente l'avvolgimento secondario, ai capi del quale si avrà la tensione e₂

$\! \! \! \! \! \! \! \! \! {\color{Red} \mathbf{ \phi _{M}=\frac{E_{1}*T}{4N_{1}}=\frac{E_{1}}{4N_{1}*f} }}$