Elettrotecnica
Rappresentazione vettoriale delle sinusoidi
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Giovedì, 15 Maggio 2014 16:39
- Scritto da Super User
- Visite: 7440
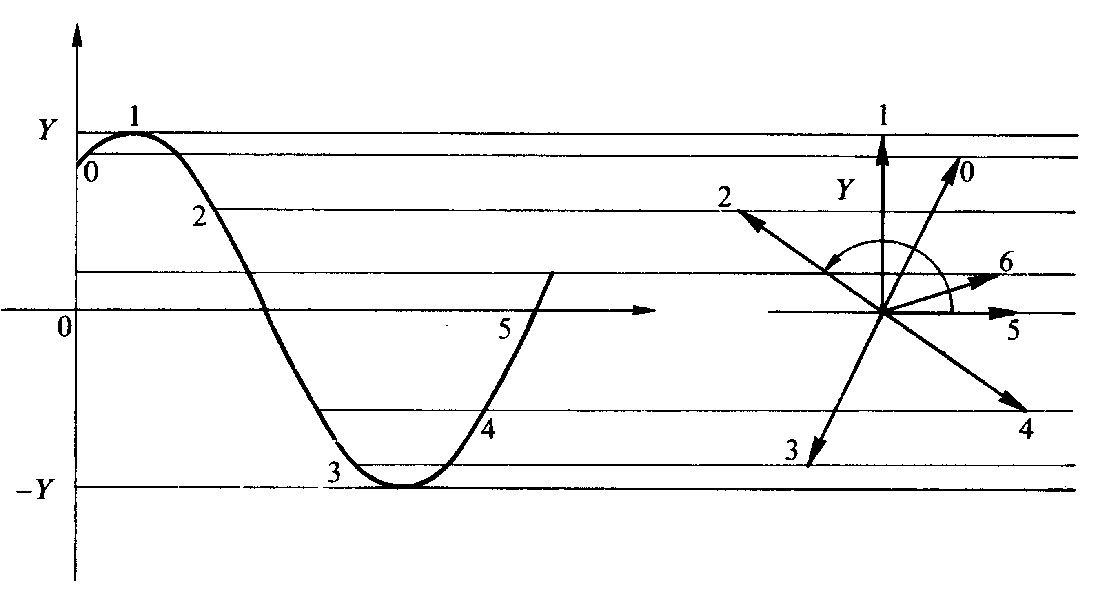
Fig 1.14 - Corrispondenza tra sinusoide e vettore
Le operazioni definite nell'articolo «Operazioni lineari sulle sinusoidi», se eseguite. punto per punto sulle sinusoidi, risultano lunghe, laboriose ed inadatte per calcoli complessi. È tuttavia possibile semplificare notevolmente la procedura di calcolo utilizzando la corrispondenza fra sinusoidi e vettori.
Operazioni lineari sulle sinusoidi
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Sabato, 10 Maggio 2014 08:50
- Scritto da Super User
- Visite: 8460
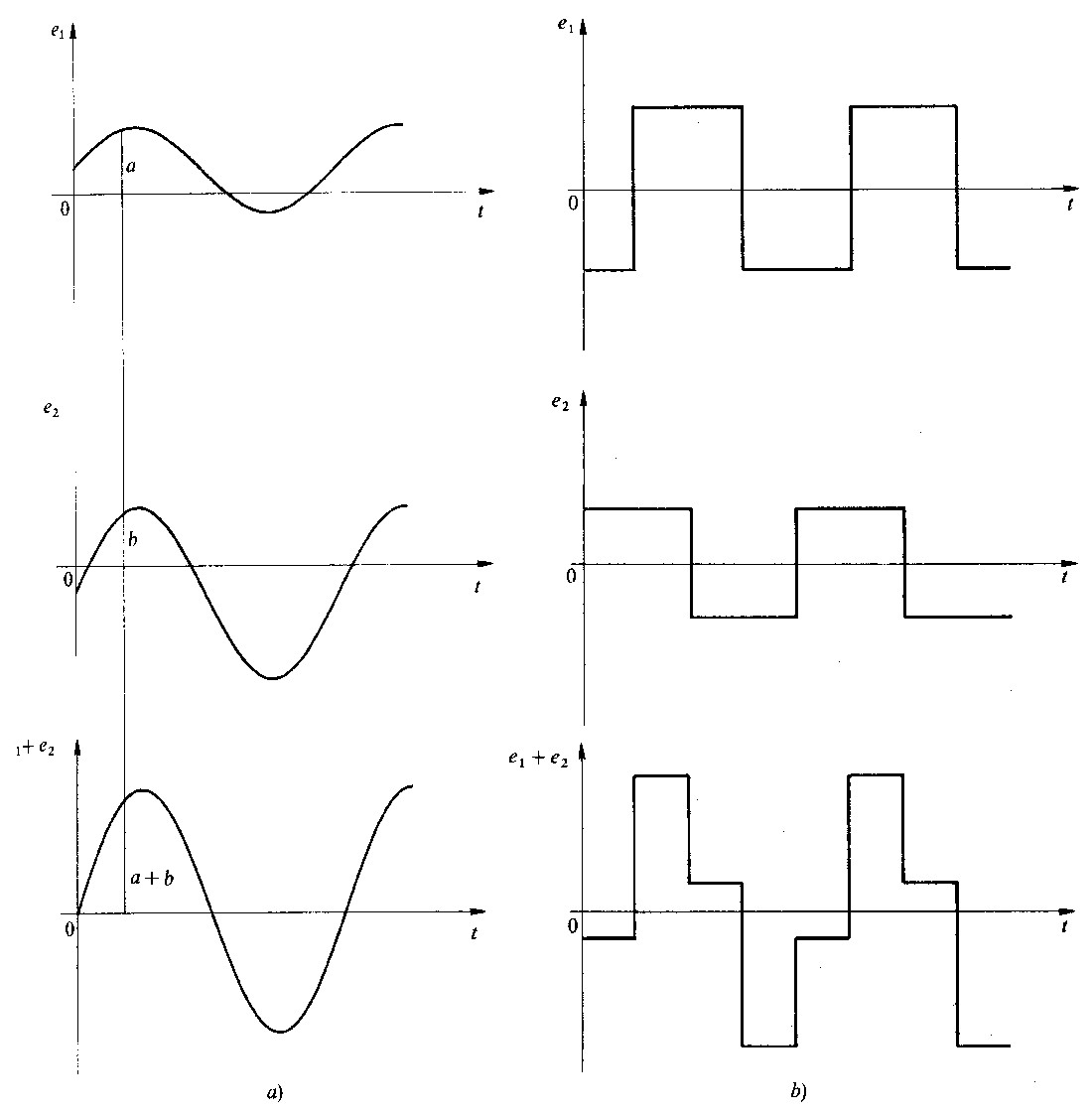
Fig 1.11 - a) somma fra sinusoidi.La somma conserva la forma degli addendi. b) Somma fra funzioni periodiche non sinusoidali. La somma non conserva la forma degli addendi
Lo studio delle reti elettriche alimentate da tensioni e correnti sinusoidali richiede l’esecuzione di operazioni fra sinusoidi. Definiamo le operazioni lineari di somma, prodotto e rotazione di fase.
Fase di una sinusoide
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Sabato, 10 Maggio 2014 06:10
- Scritto da Super User
- Visite: 7331
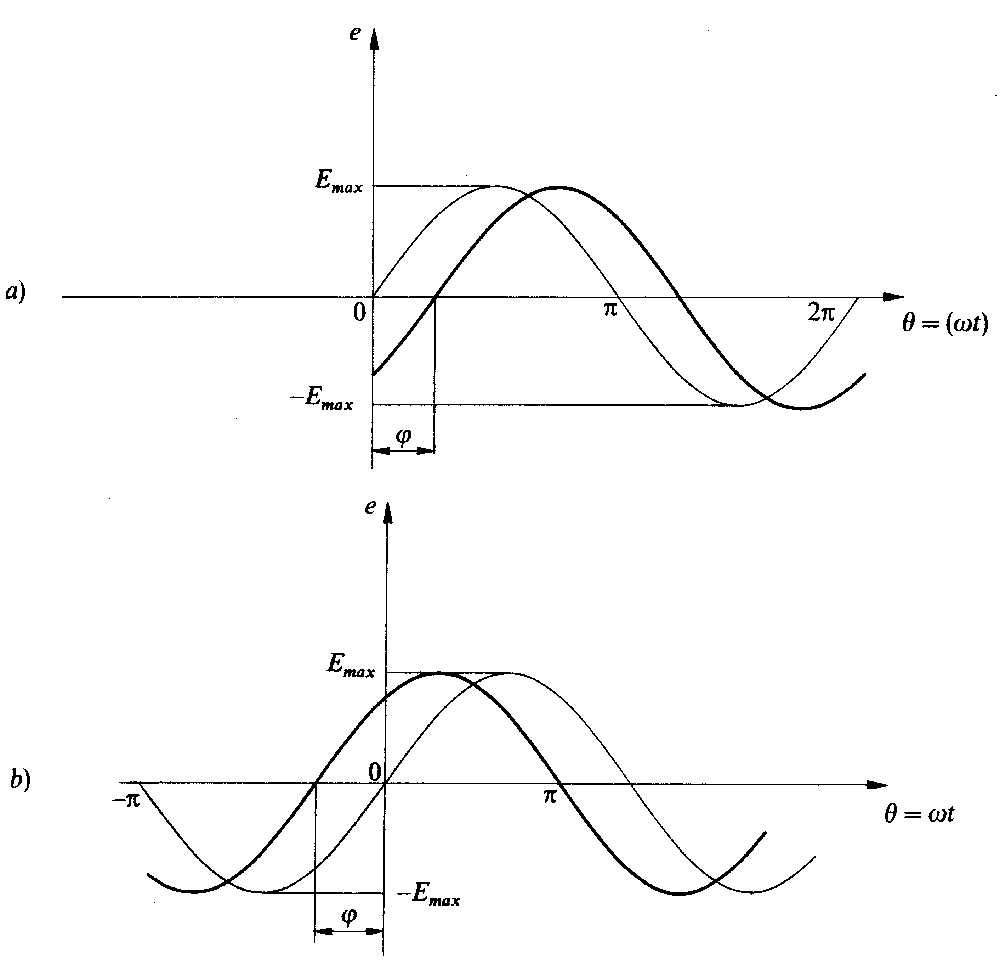
Fig 1.10 - Angolodi fase a) sinusoide in ritardo (φ negativo); b) sinusoide in anticipo (φ positivo)
La sinusoide fin qui considerata, avente espressione analitica
Funzione sinusoidale
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Martedì, 06 Maggio 2014 16:39
- Scritto da Super User
- Visite: 8043
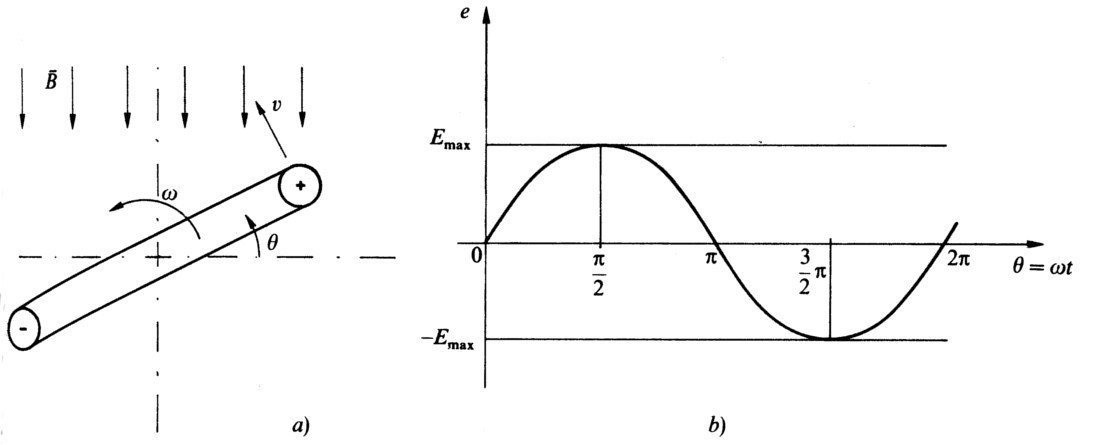
Fig 1.7 - Generazione di una tensione sinusoidale
Le reti di distribuzione dell'energia forniscono agli utenti tensione alternata di forma sinusoidale; alla funzione sinusoidale viene dedicato uno studio particolarmente approfondito. In fig. 1.7 a) è illustrato un dispositivo per generare una tensione sinusoidale: una bobina ruota in un campo magnetico uniforme con velocità ω costante; l’angolo descritto dopo il tempo t è
Fattore di forma
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Giovedì, 24 Aprile 2014 11:02
- Scritto da Super User
- Visite: 13117
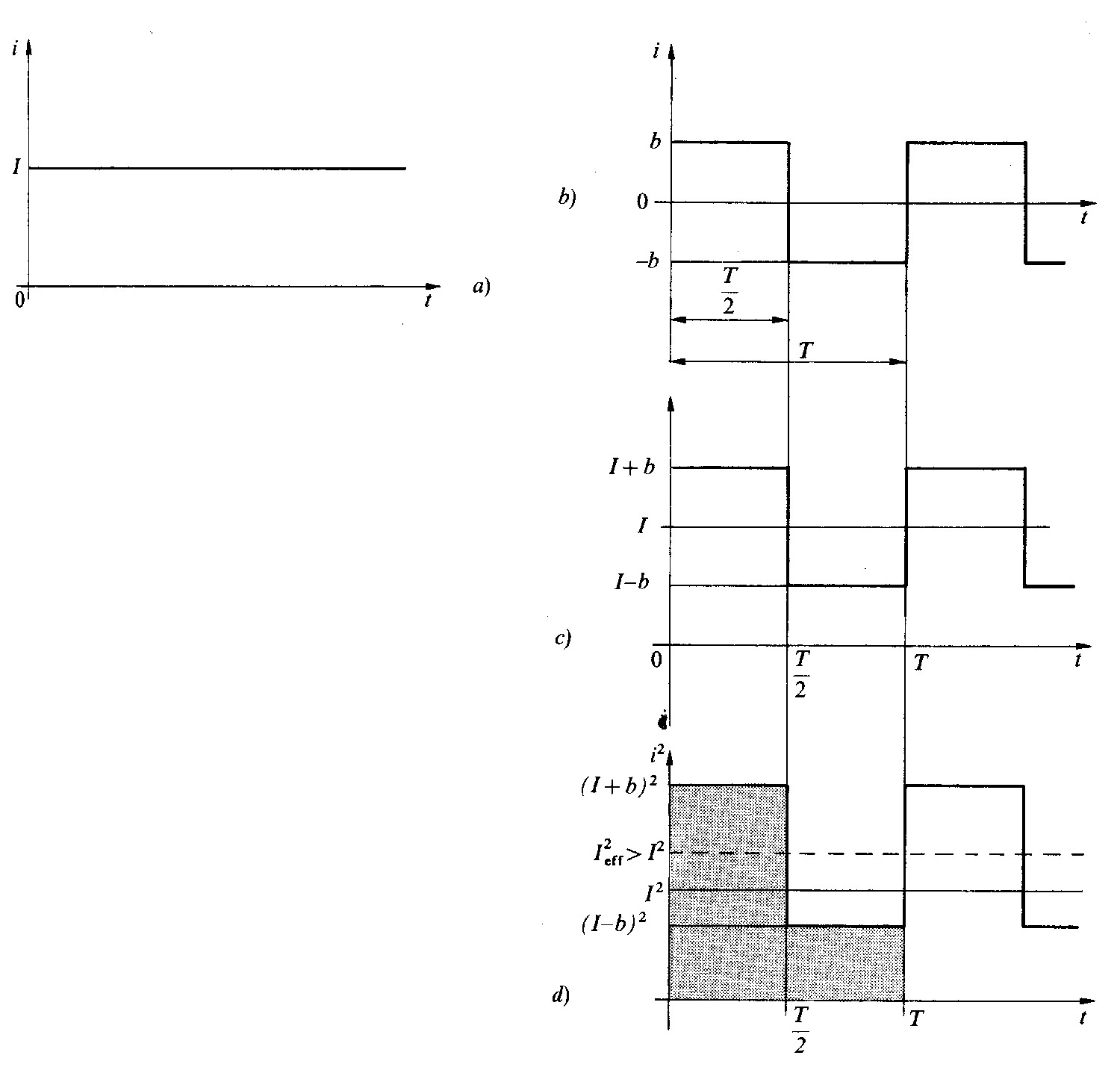
Fig 1.5 - Dimostrazione che k>1
Il rapporto fra il valore efficace di una grandezza ed il suo valor medio è detto fattore di forma e si indica con kf:
Valore Efficace
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Domenica, 20 Aprile 2014 08:23
- Scritto da Super User
- Visite: 6665
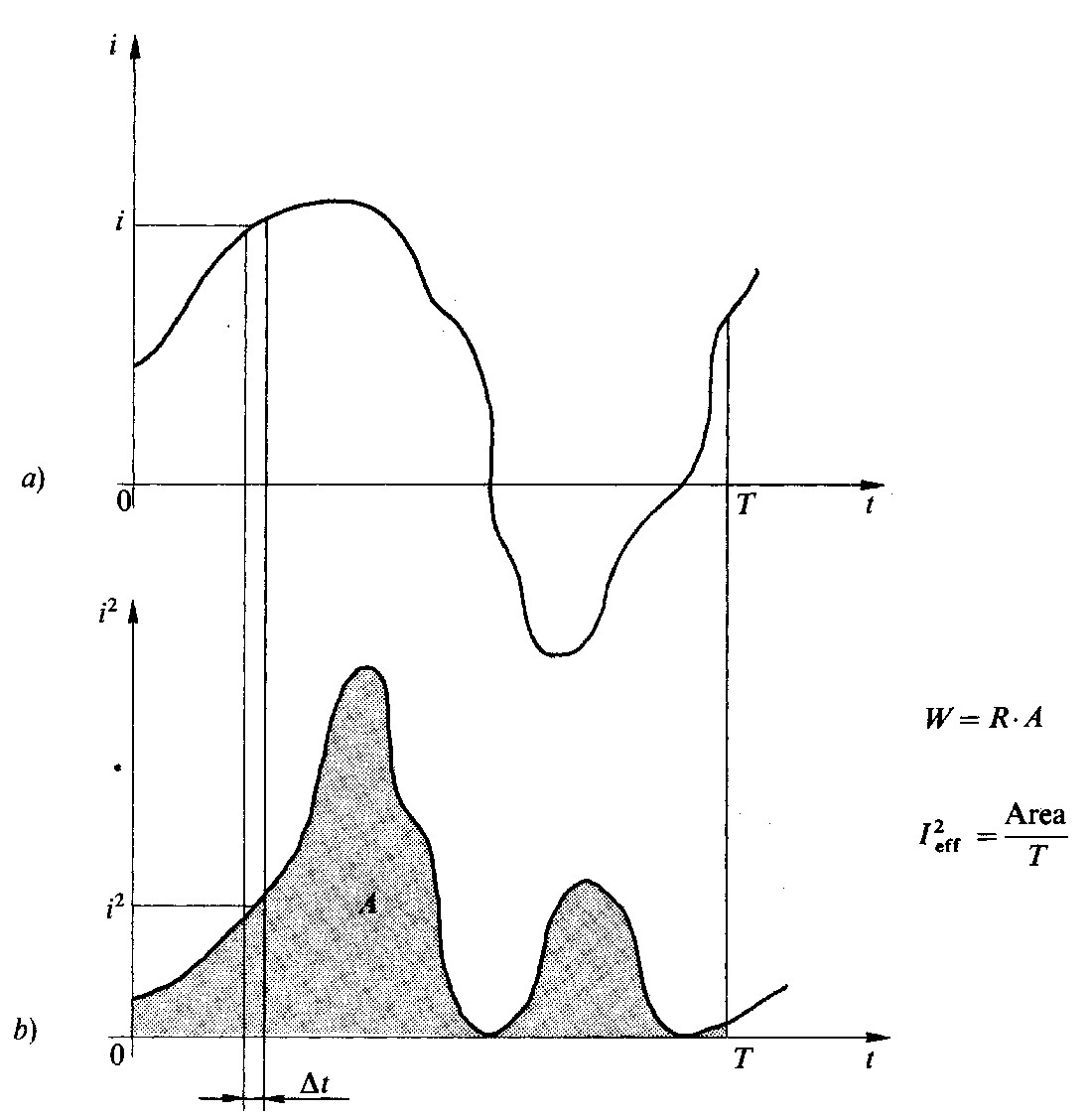
Fig 1.3 - Calcolo del valore efficace
Una corrente periodica che percorre una resistenza R dissipa, nel periodo T, una ben precisa energia W. La potenza media è data da
Funzione Periodica
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Sabato, 19 Aprile 2014 19:26
- Scritto da Super User
- Visite: 5955
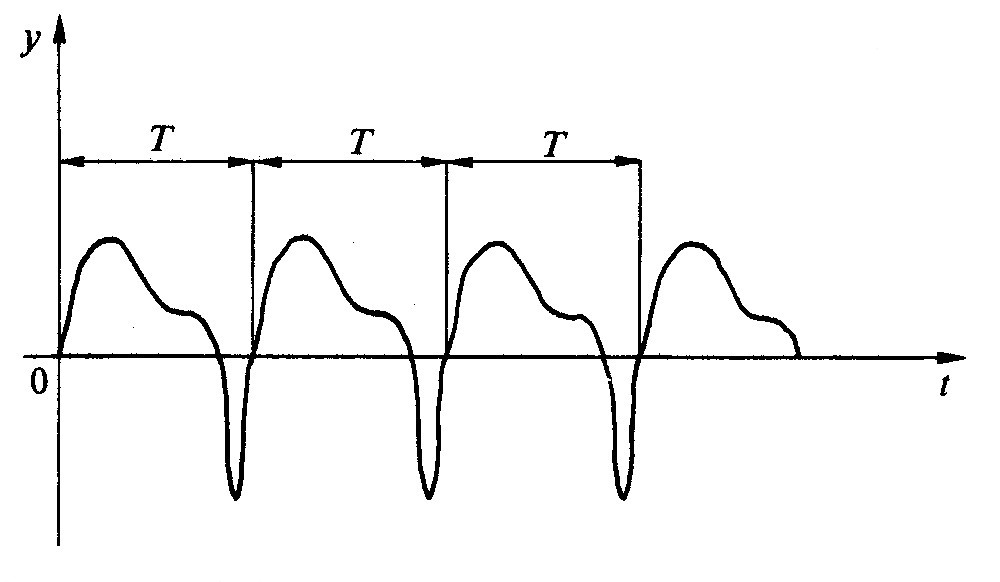
Fig 1.1 - funzione periodica
Nella parte prima sono stati esaminati circuiti alimentati con tensioni e correnti costanti nel tempo. Molti fenomeni sono tuttavia caratterizzati da correnti e tensioni variabili nel tempo, come ad esempio i transistori visti nella seconda e terza parte.
Transitori nei circuiti R - L
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Domenica, 09 Marzo 2014 12:12
- Scritto da Super User
- Visite: 10263
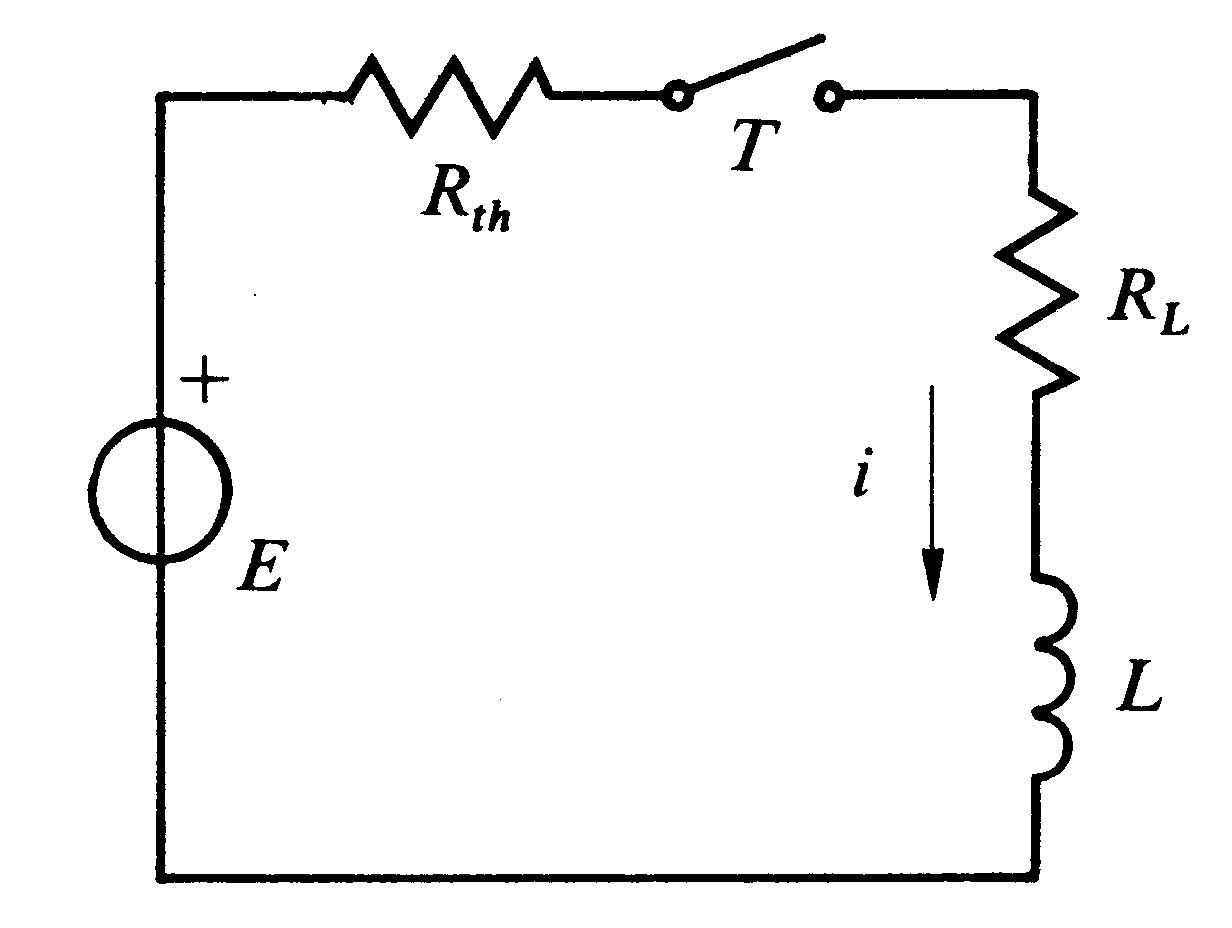
Fig 6.1 - Chiusura di un circuito induttivo
Consideriamo il circuito di fig. 6.1, dove un conduttore di induttanza L e di resistenza R L è alimentato da una rete lineare comunque complessa schematizzata, secondo il teorema di Thévenin, dalla serie di un generatore di tensione ideale e di una resistenza equivalente R,,,. La resistenza totale del circuito, vista dall'induttanza, risulta
Perdite per isteresi
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Mercoledì, 25 Dicembre 2013 14:27
- Scritto da Super User
- Visite: 11790
Nell'articolo «Energia nei circuiti magnetici» si è dimostrato che il circuito magnetico restituisce tutta l’energia immagazzinata se la caratteristica di magnetizzazione viene percorsa identicamente nei due sensi.
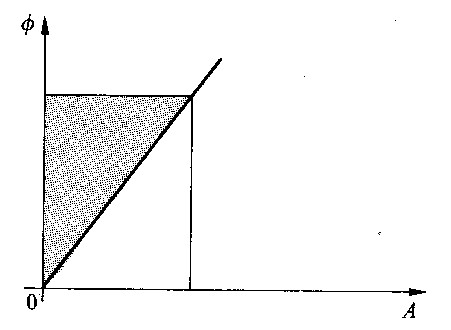
Fig 5.2 - Energia immagazzinata in un circuito magnetico lineare.
Caratteristica dei circuiti magnetici in serie
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Sabato, 21 Dicembre 2013 13:40
- Scritto da Super User
- Visite: 3947
Raramente un circuito magnetico è omogeneo come quello visto al paragrafo precedente; molto più spesso i circuiti magnetici sono composti da più tronchi diversi nelle dimensioni e nei materiali di cui sono costituiti. Occorre inoltre tener conto di quei tronchi composti da materiale non ferromagnetico, detti traferri. Più tronchi di circuito magnetico sono posti in serie quando sono percorsi dallo stesso flusso, come in fig. 4.12.
Circuiti di spegnimento
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Domenica, 16 Marzo 2014 08:15
- Scritto da Super User
- Visite: 4723
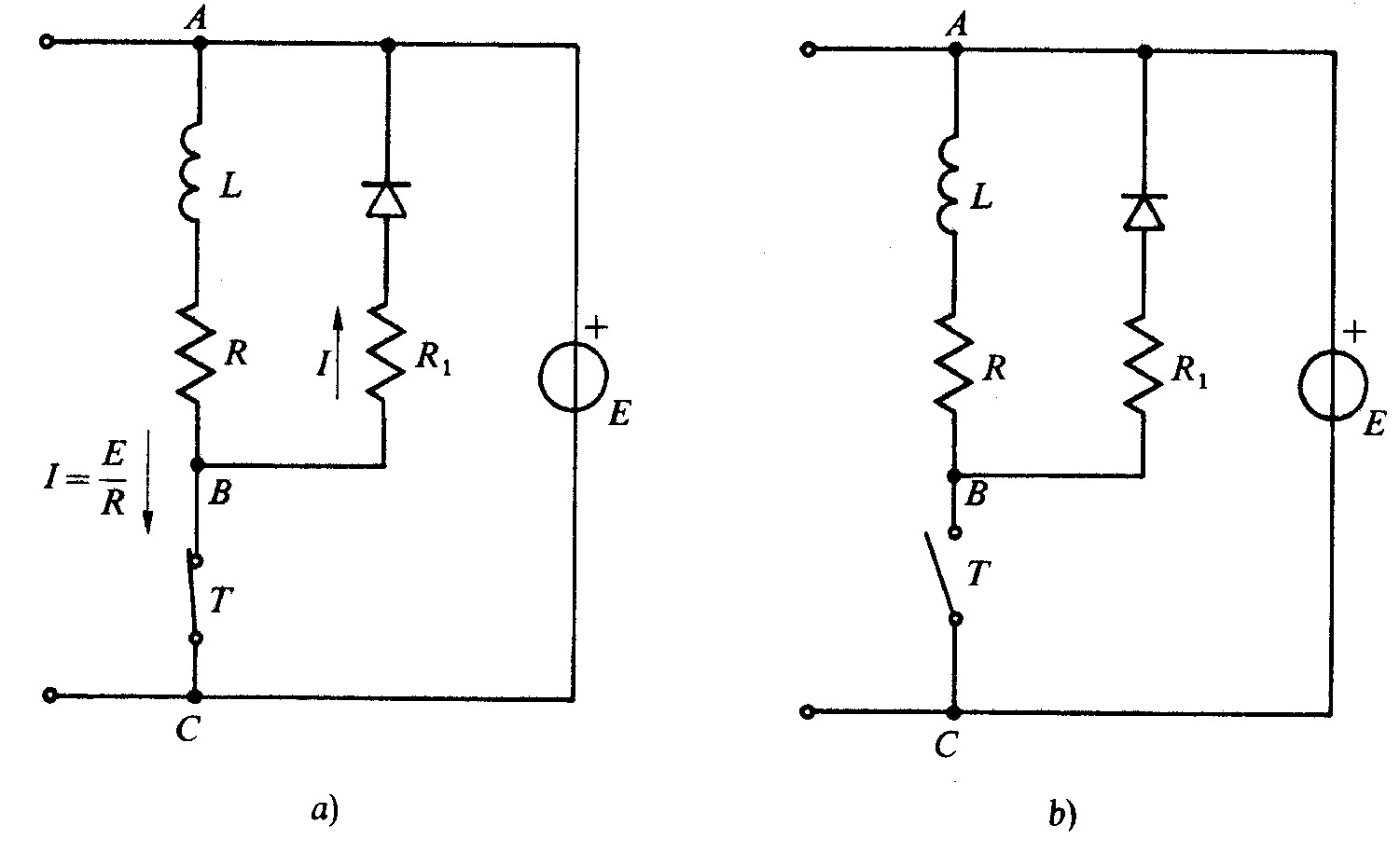
Fig 6.6 - Interruzione con dissipazione su resistenza
Proponiamo due disposizioni circuitali molto utilizzate in pratica, che permettono di limitare le sovratensioni all’interruzione dei circuiti induttivi.
Forza di attrazione di un elettromagnete
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Giovedì, 26 Dicembre 2013 10:39
- Scritto da Super User
- Visite: 14241
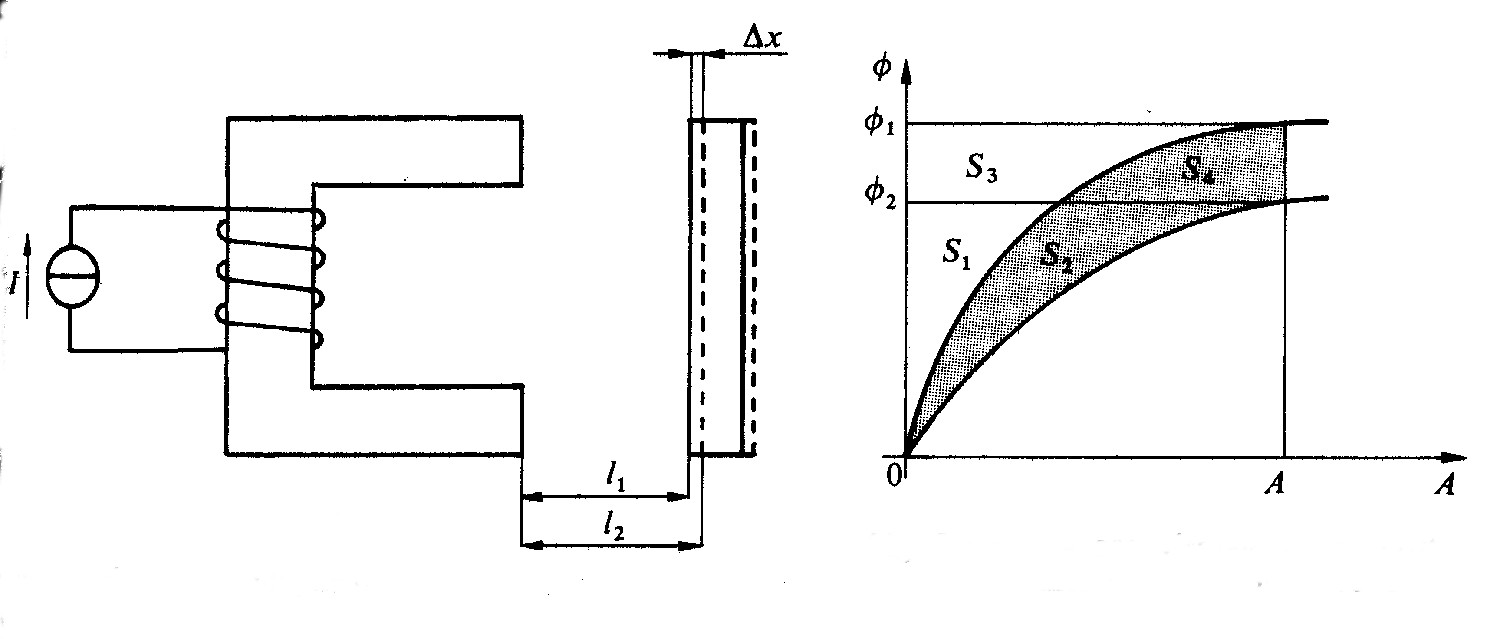
Fig 5.6 - a) Elettromagnete b) Lavoro virtuale nello spostamento dell'ancora mobile
L’elettromagnete di fig. 5.6a è alimentato da un generatore di corrente. Sappiamo per esperienza che esso esercita una forza di attrazione sull'ancora mobile di ferro: ci proponiamo ora di calcolarne il valore.
Energia nei circuiti magnetici
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Mercoledì, 25 Dicembre 2013 13:28
- Scritto da Super User
- Visite: 6991
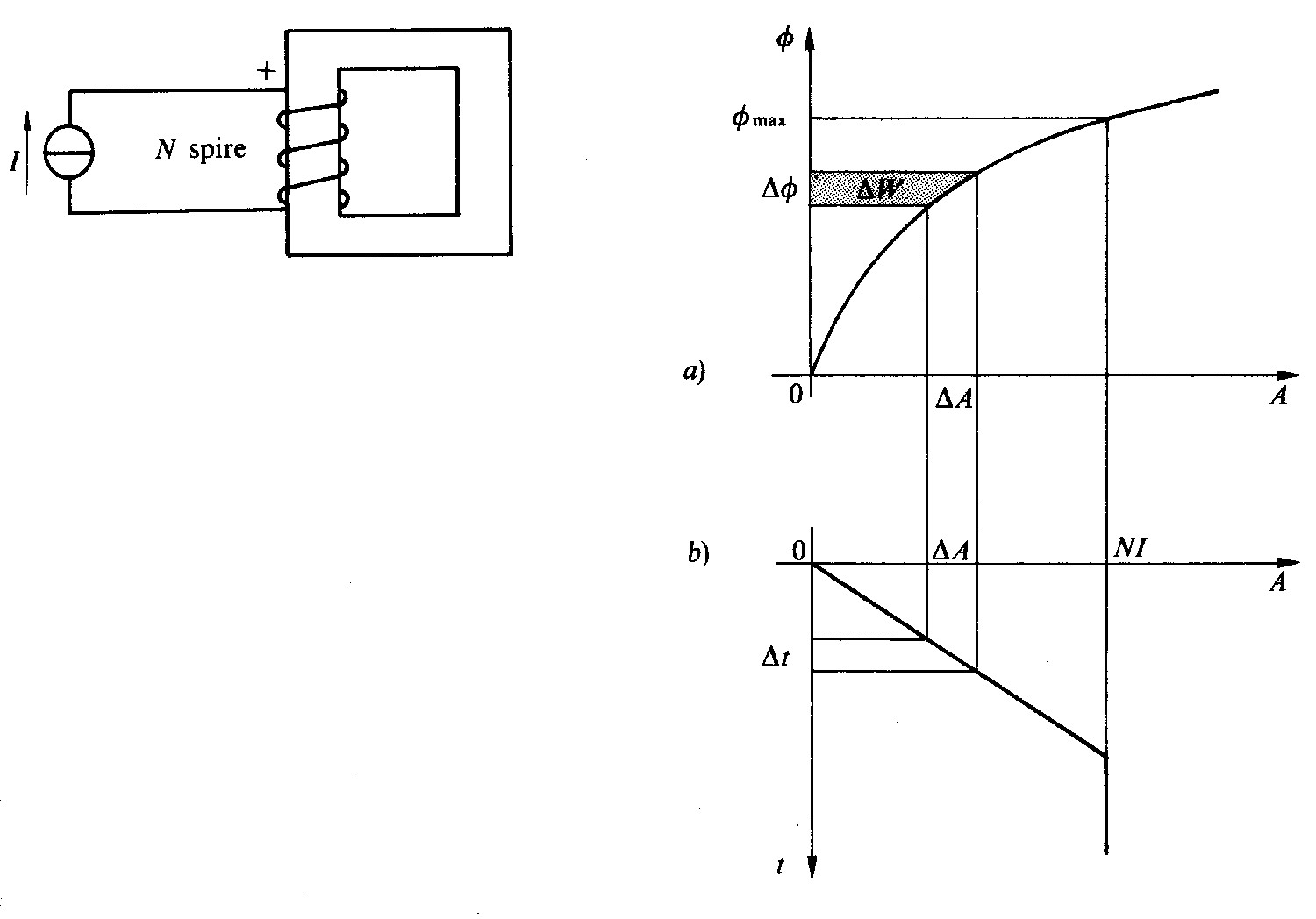
Fig 5.1 - Energia immagazzinata in un circuito magnetico
Nella disposizione sperimentale di fig. 5.1 si suppone che l’avvolgimento sia privo di resistenza ed abbia N spire; la caratteristica del circuito magnetico è data dal grafico a).
Calcolo dei circuiti magnetici
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Domenica, 15 Dicembre 2013 08:40
- Scritto da Super User
- Visite: 5876
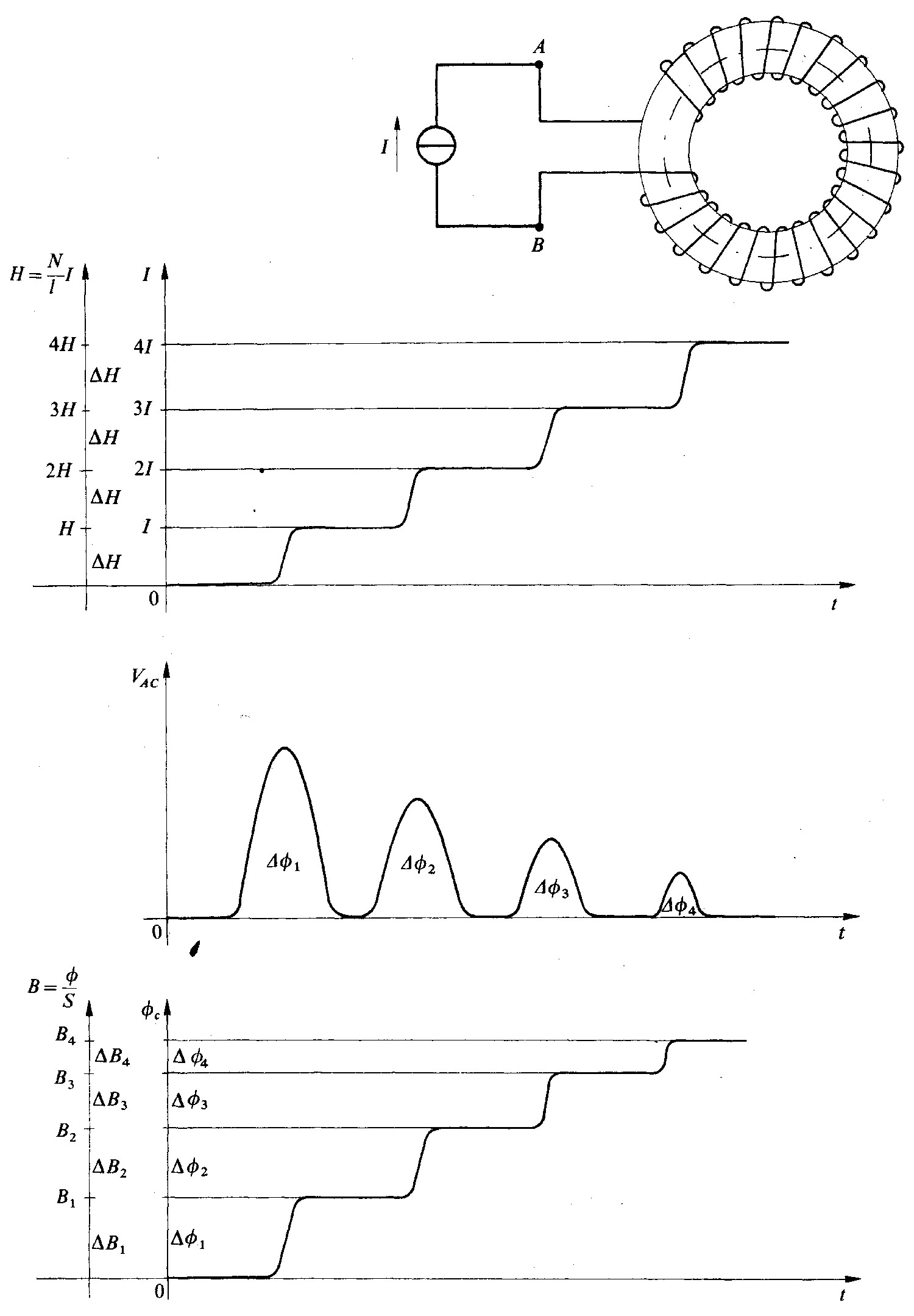
Prendiamo ancora in esame il circuito magnetico toroidale omogeneo illustrato in fig. 4.2 illustrato nell'articolo caratteristica di magnetizzazione; il materiale che ne costituisce il nucleo presenta la caratteristica H-B riportata in fig. 4.10 a).
Apertura di un circuito induttivo
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Sabato, 15 Marzo 2014 09:13
- Scritto da Super User
- Visite: 5659
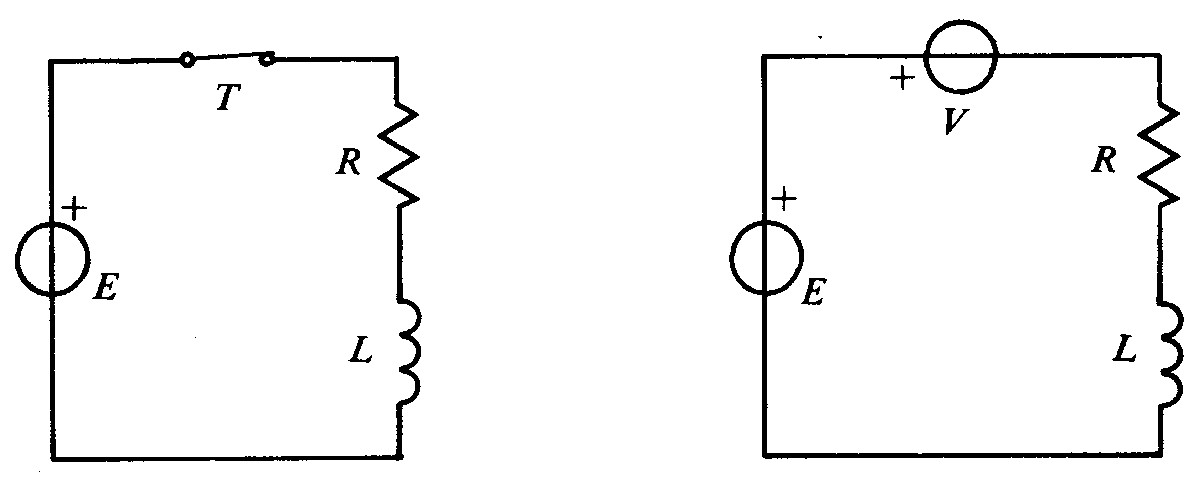
Fig 6.3 - a) Apertura di un circuito induttivo, - b) Schematizzazione dell'arco elettrico all'apertura di un circuito induttivo
Il circuito di fig. 6.3 a), chiuso da tempo illimitato, è percorso dalla corrente I = E/R e l’energia immagazzinata nell'induttore vale W= 1/2 LI2.
Ad un certo istante si apre il tasto T, con l’intenzione di interrompere la corrente, ma per il principio di continuità, il valore della corrente immediatamente dopo l’apertura del tasto sarà ancora uguale ad I, anche se decrescente.
Correnti parassite
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Giovedì, 26 Dicembre 2013 09:21
- Scritto da Super User
- Visite: 8935
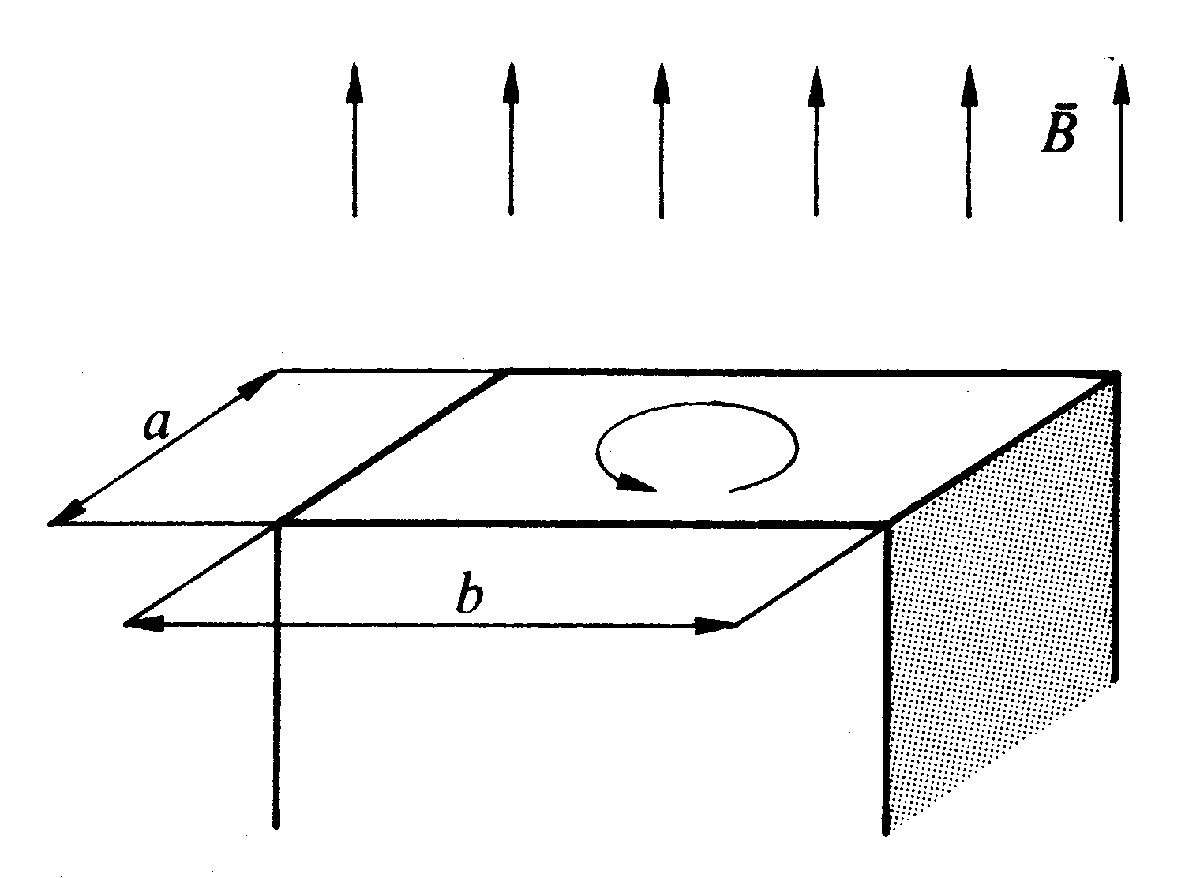
Fig 5.4 - Andamento delle correnti parassite in un nucleo massiccio
Rapide variazioni di flusso inducono tensioni nello spazio e nei materiali circostanti (vedersi articolo «Calcolo della tensione indotta come variazione di flusso»). Anche nei nuclei magnetici interessati da flussi variabili nel tempo vengono indotte tensioni come in fig. 5.4.
Caratteristica dei circuiti magnetici in parallelo
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Sabato, 21 Dicembre 2013 14:38
- Scritto da Super User
- Visite: 4161
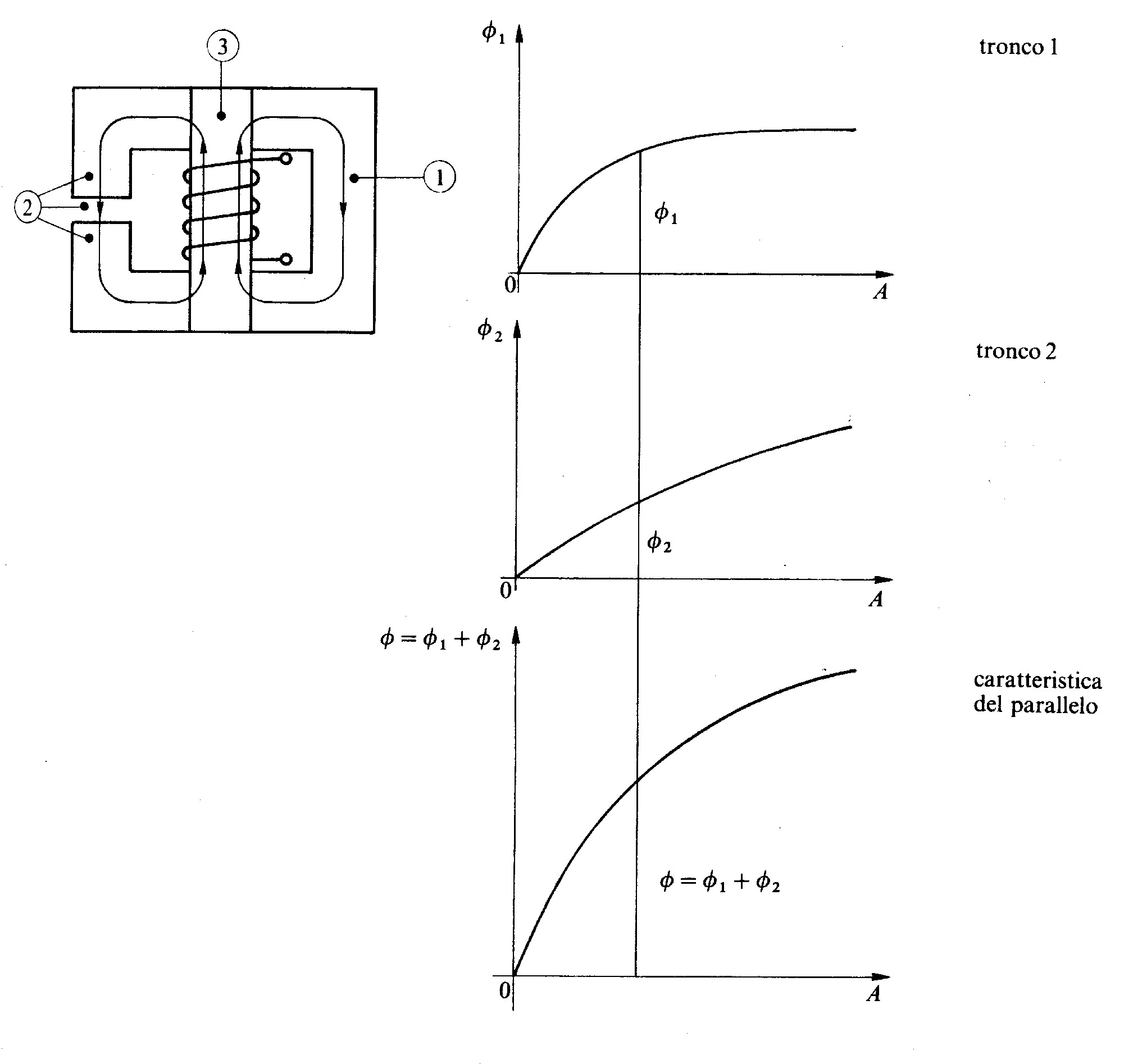
Fig 4.14 - Metodo grafico per ricavare la caratteristica di un circuito magnetico composto da più tronchi in parallelo
Nel circuito magnetico di fig. 4.14 il flusso si suddivide nei due tronchi in parallelo, indicati con 1 e 2, dei quali sono note le caratteristiche, riportate
nelle figure a) e b). Il tronco 2 è composto a sua volta da più parti in serie, e ne viene data la caratteristica totale, la quale, a causa del1’ampio traferro,
presenta un ginocchio poco pronunciato.
Leggi tutto: Caratteristica dei circuiti magnetici in parallelo
Diversi tipi di materiali magnetici
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Venerdì, 06 Dicembre 2013 08:27
- Scritto da Super User
- Visite: 12498
I diversi materiali presentano cicli di isteresi differenti, ma sempre chiusi e simmetrici se si adottano valori simmetrici di Hmax; in particolare (fig. 4.5) si distinguono materiali magnetici dolci (a) caratterizzati da cicli stretti: il valore di Br può essere elevato, ma il valore di Hc, è sempre molto basso ed il materiale si smagnetizza facilmente; tali sono i metalli ferromagnetici puri (ferro con basso tenore di carbonio, nichel, cobalto), alcune leghe appositamente realizzate (ad esempio mumetal, permalloy) e le ferriti dolci (ossidi di metalli ferromagnetici).
Altri articoli...
- Caratteristica di magnetizzazione
- Materiali ferromagnetici
- Calcolo dell'induttanza di un solenoide
- Energia immagazinata nel campo magnetico
- Autoinduttanza
- Tensione indotta in una bobina senza movimento meccanico - Mutua induttanza
- Tensione indotta in una spira rigida di movimento
- Tensione indotta come derivata del flusso
- L'autoparlante
- Calcolo della tensione indotta come variazione di flusso
- Flusso Magnetico
- Coppia in una spira immersa in un campo magnetico
- Forze meccaniche fra correnti
- Solenoide
- Schiera di N conduttori paralleli
- Campo generato dalla presenza contemporanea di più conduttori
- Campo magnetico prodotto dalla corrente
- Moto di un elettrone in un campo magnetico
- Tensione indotta in un conduttore
- Costante Elettromeccanica