Elettrotecnica
Caratteristica di magnetizzazione
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Domenica, 01 Dicembre 2013 07:56
- Scritto da Super User
- Visite: 14970
Il valore di μ nei materiali magnetici non è costante, ma varia in funzione del livello di induzione B a cui si trova il materiale. La caratteristica B-H non è perciò lineare.
Per ricavarla sperimentalmente supponiamo di avere un anello di materiale ferromagnetico, come in fig. 4.2, sul quale siano avvolte uniformemente N spire in serie di resistenza trascurabile. Inizialmente la bobina non è percorsa da alcuna corrente; si porta poi la corrente al valore I: una generica linea di induzione all'interno del materiale sarà dunque sottoposta ad una correnteconcatenata A pari a N*I; l’intensità del campo sarà allora
Materiali ferromagnetici
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Domenica, 24 Novembre 2013 17:49
- Scritto da Super User
- Visite: 7048
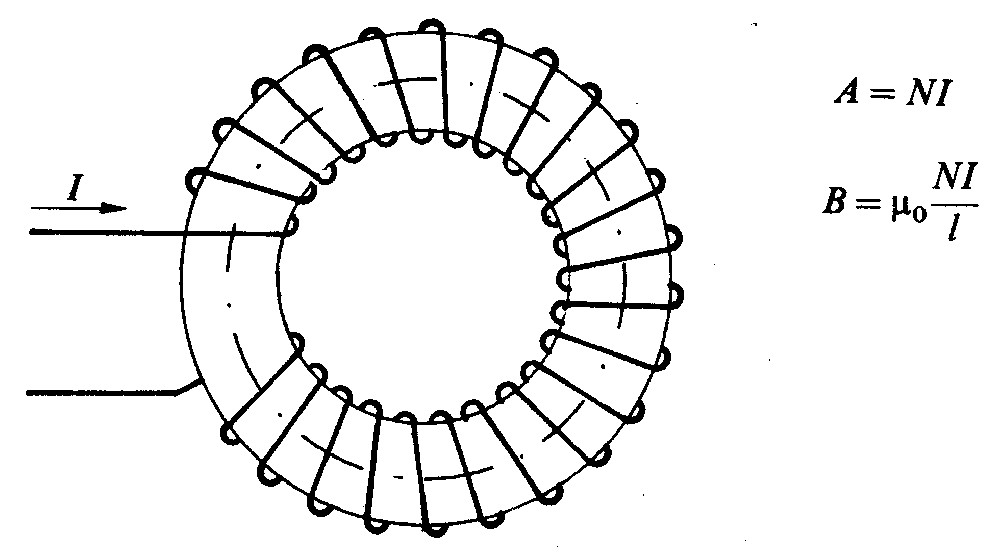
Fig 4.1 - Solenoide toroidale
Consideriamo il solenoide di fig. 4.1, curvato in modo da formare un anello o toro; la lunghezza l del solenoide viene a coincidere con la lunghezza dell'asse indicato in figura con tratto e punto. Abbiamo già visto nell'articolo Solenoide che l’induzione all’esterno è praticamente nulla, mentre all'interno del solenoide vale:
Calcolo dell'induttanza di un solenoide
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Martedì, 19 Novembre 2013 20:16
- Scritto da Super User
- Visite: 30386
Consideriamo un solenoide avente lunghezza l, diametro d piccolo rispetto a l, e numero di spire N. La sua sezione trasversale ha area S data dall'espressione
Energia immagazinata nel campo magnetico
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Sabato, 16 Novembre 2013 10:07
- Scritto da Super User
- Visite: 4890
Il circuito di fig. 3.13 a), di resistenza trascurabile, ha induttanza L (qualsiasi circuito presenta sempre un certo valore di induttanza, poiché la corrente genera sempre un campo magnetico).
Autoinduttanza
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Sabato, 16 Novembre 2013 09:25
- Scritto da Super User
- Visite: 8312
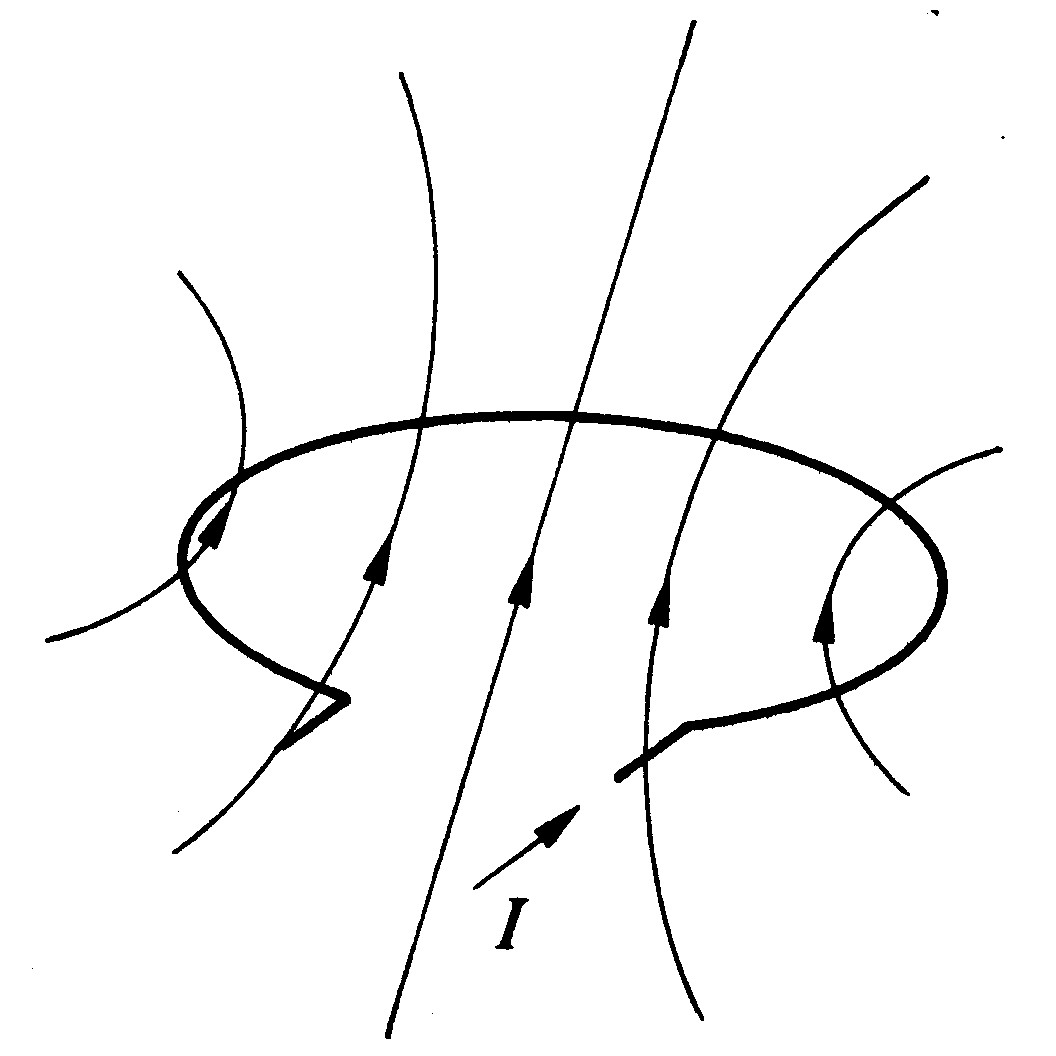
Fig 3.10 - Autoinduttanza
Un circuito chiuso percorso da corrente genera un campo magnetico; variazioni di corrente producono variazioni di flusso che possono indurre tensioni in altri circuiti, ma soprattutto inducono tensione nel circuito stesso. Supponiamo che il circuito di fig. 3.10, di resistenza trascurabile, percorso dalla corrente I, generi il flusso Φ concatenato con se stesso. Se il circuito è costituito da una bobina di N spire il flusso concatenato sarà, come al solito,
Tensione indotta in una bobina senza movimento meccanico - Mutua induttanza
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Domenica, 10 Novembre 2013 20:22
- Scritto da Super User
- Visite: 5941
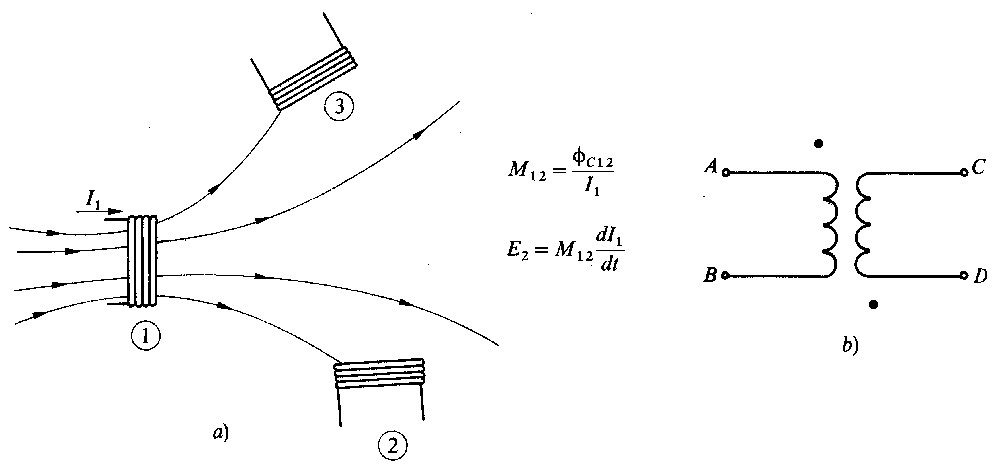
Fig 3.9 - Mutua induttanza
Negli articoli precedenti sono state considerate variazioni di flusso concatenato dovute a variazioni della geometria della spira, oppure a movimenti relativi fra bobine e campi magnetici. È tuttavia possibile variare il flusso concatenato con una bobina senza alcun movimento: basti pensare al flusso prodotto da una corrente, il quale varia ogni volta che il valore della corrente viene modificato.
Leggi tutto: Tensione indotta in una bobina senza movimento meccanico - Mutua...
Tensione indotta in una spira rigida di movimento
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Martedì, 05 Novembre 2013 21:30
- Scritto da Super User
- Visite: 6650
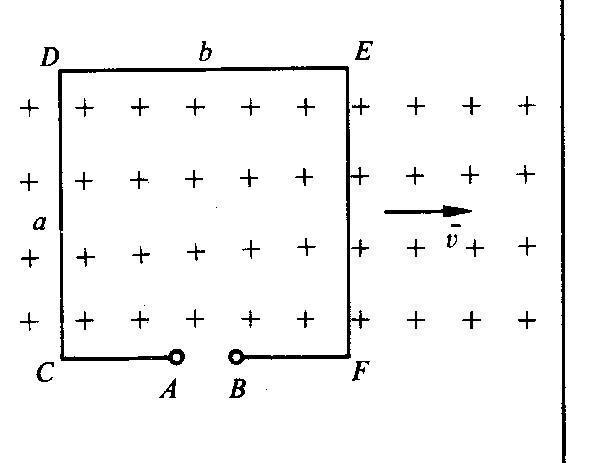
Fig 3.6 - Tensione indotta in una spira rigida in movimento.
Consideriamo la spira rigida, avente lati di lunghezza a e b, area S = a*b, di fig. 3.6. Essa è perpendicolare all’induzione uniforme B, presente nella parte sinistra dello spazio considerato, mentre nella parte destra l’induzione è nulla.
Leggi tutto: Tensione indotta in una spira rigida di movimento
Calcolo della tensione indotta come variazione di flusso
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Lunedì, 14 Ottobre 2013 07:02
- Scritto da Super User
- Visite: 10858

Fig 3.3 - Variazione di flusso dovuta al movimento di un conduttore
Leggi tutto: Calcolo della tensione indotta come variazione di flusso
Forze meccaniche fra correnti
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Domenica, 06 Ottobre 2013 12:41
- Scritto da Super User
- Visite: 4043
Si è visto al paragrafo precedente che una corrente è circondata da un campo magnetico; una seconda corrente immersa in tale campo è sottoposta ad una forza meccanica (ci siamo serviti proprio di questo fenomeno per misurare B in ogni punto). Possiamo quindi affermare che due conduttori di lunghezza l, affacciati alla distanza d, percorsi da corrente si scambiano una forza meccanica. Le formule viste finora sono sufficienti per il calcolo di tale forza.
Campo generato dalla presenza contemporanea di più conduttori
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Venerdì, 27 Settembre 2013 20:05
- Scritto da Super User
- Visite: 4165
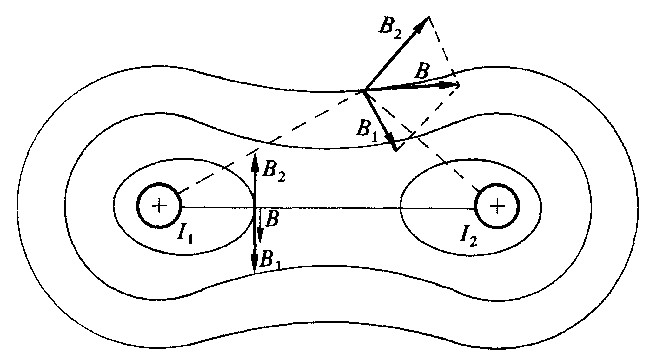
Fig 2.3 - Campo prodotto da due conduttori percorsi da corrente nello stesso senso
Leggi tutto: Campo generato dalla presenza contemporanea di più conduttori
Tensione indotta come derivata del flusso
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Domenica, 27 Ottobre 2013 07:16
- Scritto da Super User
- Visite: 5270
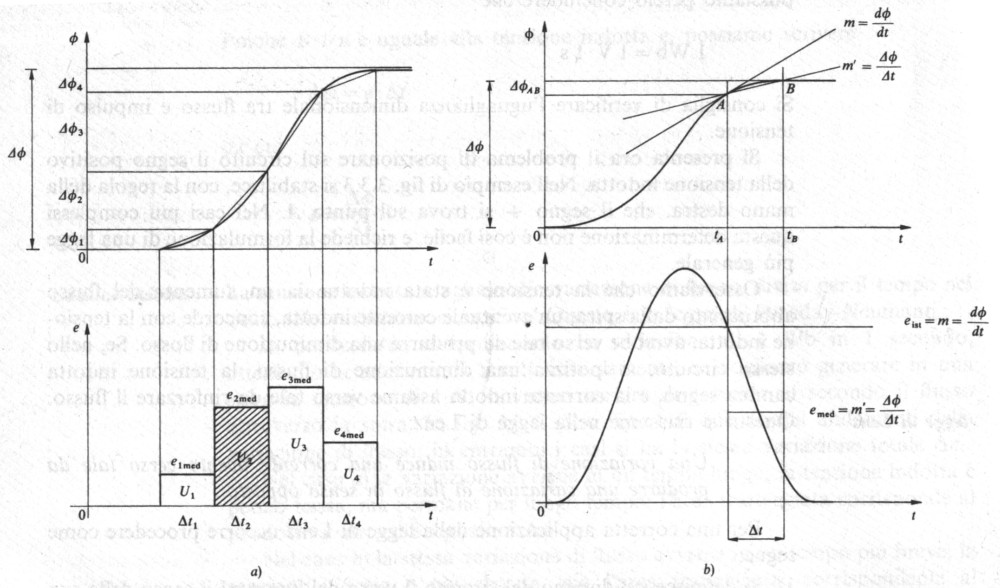
Fig 3.5 - Tensione indotta, come derivata del flusso rispetto al tempo
Flusso Magnetico
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Domenica, 13 Ottobre 2013 17:56
- Scritto da Super User
- Visite: 6370
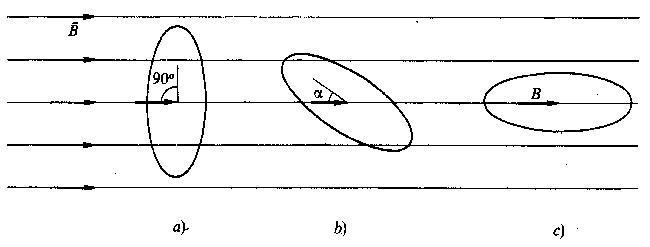
Fig 3.1 - Flusso attraverso una superficie
Consideriamo un campo magnetico uniforme, avente induzione B costante. Isoliamo‘ una superficie di area S, perpendicolare a B, come la superficie a) di fig. 3.1. Il prodotto B*S definisce una nuova grandezza, detta flusso magnetico (simbolo Φ).
Solenoide
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Venerdì, 04 Ottobre 2013 15:13
- Scritto da Super User
- Visite: 6870
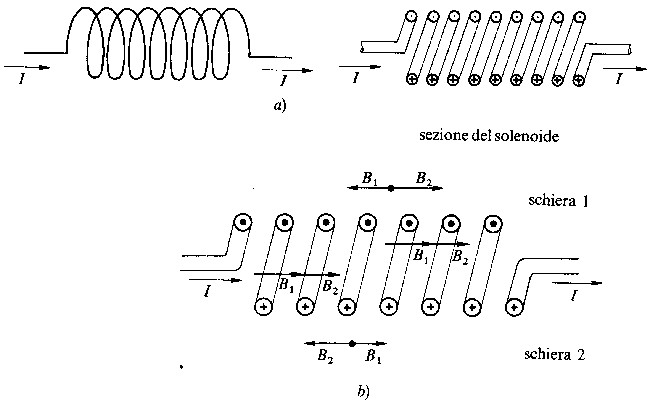
Fig 2.7 - Solenoide percorso da corrente
Campo magnetico prodotto dalla corrente
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Giovedì, 26 Settembre 2013 16:20
- Scritto da Super User
- Visite: 7033
Nel capitolo precedente abbiamo visto come, in presenza di un campo magnetico, sono osservabili azioni ben precise sulle correnti elettriche e sui conduttori in moto; abbiamo utilizzato proprio queste azioni per definire il vettore B e la relativa unità di misura (tesla), ma non abbiamo ancora trattato il modo di generare il campo magnetico stesso. Questo studio sarà l’oggetto dei presenti articoli.
L'autoparlante
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Giovedì, 17 Ottobre 2013 10:13
- Scritto da Super User
- Visite: 16221
Potrà essere capitato, almeno qualche volta, di consultare un listino commerciale in cui vengono presentati vari tipi di altoparlanti e di accorgersi che il costruttore preferisce indicare il peso del cestello anziché quello del magnete. Questo dato non deve trarre in inganno il principiante, pensando che il costruttore, presentando un peso superiore, voglia impressionare gli acquirenti. Infatti, un altoparlante di grande classe, equipaggiato con un cestello di una certa mole, viene a costare molto di più di un altoparlante nel quale il magnete permanente non è racchiuso in un contenitore vero e proprio. Con ciò si vuol dire che l’insieme degli elementi che racchiudono il magnete, viene a costare di più del magnete stesso. Per giustificare questa asserzione occorre esaminare attentamente la struttura di un altoparlante.
Coppia in una spira immersa in un campo magnetico
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Lunedì, 07 Ottobre 2013 20:26
- Scritto da Super User
- Visite: 5384
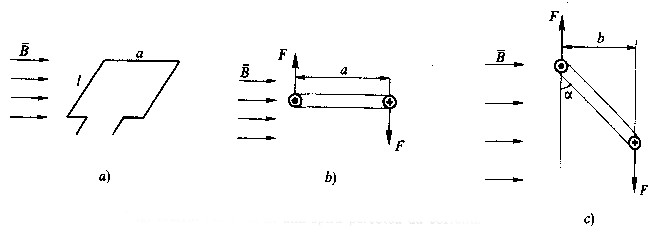
Fig 2.11 - Coppia in una spira percorsa da corrente
Leggi tutto: Coppia in una spira immersa in un campo magnetico
Schiera di N conduttori paralleli
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Venerdì, 04 Ottobre 2013 14:44
- Scritto da Super User
- Visite: 3961
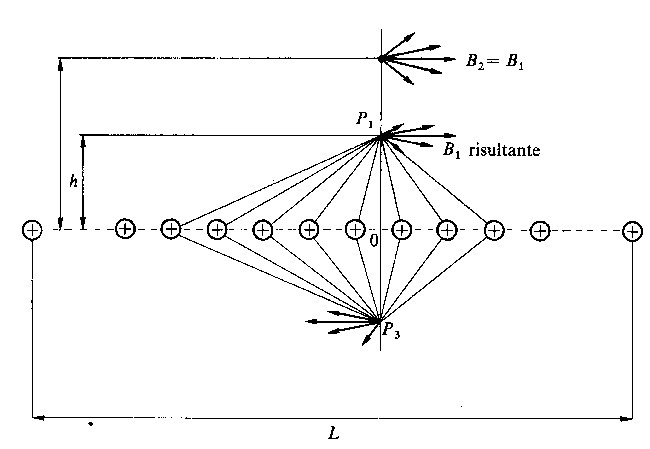
Fig 2.6 - Schiera di N conduttori paralleli
Moto di un elettrone in un campo magnetico
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Domenica, 08 Settembre 2013 08:09
- Scritto da Super User
- Visite: 13110
Un elettrone libero nel vuoto, che viaggia alla velocità v, entra in un campo magnetico uniforme avente induzione B perpendicolare alla direzione del moto, come in fig. 1.7. Come è noto, l’elettrone possiede una carica e = 1,602*1O-19 C; un elettrone in moto, che percorre un minuscolo tratto di lunghezza l nel tempo t, equivale ad una corrente
Altri articoli...
- Tensione indotta in un conduttore
- Costante Elettromeccanica
- Campo magnetico - Definizione del vettore induzione magnetica
- Scambi di energia durante la carica e la scarica del condensatore
- Caso generale di carica del condensatore
- Carica del condensatore per mezzo di un generatore reale
- Curve Esponenziali
- Principio di continuità
- Collegamenti fra condensatori
- Forza di attrazione fra le armature di un condensatore
- Energia immagazzinata nel condensatore
- Carica del condensatore per mezzo del generatore di corrente
- Rigidità Dielettrica
- Dielettrico
- Capacità - Condensatore
- Moto di un elettrone in direzione trasversale al campo elettrico
- Moto di un elettrone in direzione parallela al campo elettrico
- Presenza di un conduttore all'interno di un campo elettrico
- Superfici Equipotenziali
- Energia e potenziale