Resistori - Generalità e caratteristiche
- Dettagli
- Categoria: Resistenze
- Pubblicato Mercoledì, 14 Agosto 2013 14:55
- Scritto da Super User
- Visite: 15848
Generalità
Gli elementi di circuito che presentano fra i loro terminali una resistenza elettrica costante nominalmente, cioè quando si trascurano le inevitabili variazioni dovute alle condizioni di lavoro e ambientali, sono comunemente denominati resistori fissi. Per un conduttore di lunghezza l, sezione trasversale costante di area A, avente una resistività p (ohm-metro), la resistenza elettrica R è:
Se l’area della sezione del conduttore varia secondo la lunghezza x, la resistenza è data approssimativamente dall'espressione:
Esiste una grande varietà di tipi di resistori fissi che differiscono fra loro per la struttura e la natura dell'elemento resistivo (ad esempio: resistori a filo, a composizione di carbone, a film conduttivo), ognuno dei quali ha un suo campo di più adatta utilizzazione. I campi di utilizzazione specifici dipendono in gran parte dai seguenti fattori caratteristici: coefficiente di temperatura; potenza nominale dissipabile; coefficiente di tensione; tolleranza sul valore nominale della resistenza; tensione massima nominale; stabilità; rumore; comportamento in frequenza.
Poiché i resistori sono di per sé produttori di calore, in quanto dissipano in calore la potenza elettrica per effetto Joule, è molto importante la loro abilità di mantenere stabile il valore della resistenza su un ampio campo di temperature. Per i resistori di tipo comune, dato che normalmente le relazioni che legano la temperatura e la resistenza non sono lineari, non può essere definito un coefficiente di temperatura nel senso ordinario del termine. Si usa il termine «coefficiente» per indicare una variazione che è piccola o essenzialmente lineare, mentre viene usata la «caratteristica di temperatura» per definire una grande variazione non lineare, soprattutto per i resistori a composizione di carbone.
Per variazioni di temperatura piccole, entro le quali è possibile ritenere che, in prima approssimazione, la resistenza di un resistore vari linearmente con la temperatura, si può scrivere:
in cui R è la resistenza alla temperatura T, R0 la resistenza ad una temperatura di riferimento T0 e α il coefficiente di temperatura (α=ΔR/R ΔT), in generale funzione sia di R0 sia di T0.
Il coefficiente di temperatura viene usualmente espresso in %/°C o in parti per milione/°C (ppm/°C). Occorre notare che i valori del di temperatura sono validi soltanto entro il campo di temperature specificato e sono definiti per la temperatura media del corpo del resistore, piuttosto che per la temperatura dell'aria circostante. Nella determinazione del coefficiente di temperatura deve, perciò, essere incluso l'autoriscaldamento dovuto alla potenza dissipata dal resistore.
Il carbone, usato come elemento resistivo, ha generalmente un coefficiente di temperatura negativo, mentre i metalli tendono ad avere coefficienti positivi. Tuttavia sono state formulate alcune leghe per avere valori nulli o leggermente negativi del coefficiente di temperatura.
Potenza nominale dissipabile (Power rating)
Le caratteristiche strutturali di ogni resistore pongono un limite ben definito alla temperatura che il corpo del resistore stesso può raggiungere senza che ne derivi un danneggiamento. Pertanto resta limitata la sovraelevazione di temperatura rispetto all'ambiente che il resistore può sopportare, in dipendenza dalla potenza dissipata in calore. Si può, quindi, definire «potenza nominale dissipabile» per un certo tipo di resistore la potenza che in, esso può essere dissipata senza che si manifestino alterazioni permanenti nella sua struttura, riferendosi al funzionamento in aria libera a 25°C.
I resistori usati nei circuiti elettronici sono usualmente raffreddati per mezzo della convezione naturale dell'aria di ambiente circostante. La temperatura T del resistore e la temperatura TA di ambiente sono legate alla potenza dissipata PD tramite la resistenza termica θRA fra resistore e ambiente, secondo larelazione:
Ad esempio, per i resistori a composizione di carbone normalmente usati,θRA ≈150, 90 e 44 °K/W per i tipi rispettivamente da 1/4 Watt, 1/2 W e 1 W.
La potenza nominale fornita dal fabbricante è generalmente basata su una vita utile del resistore maggiore di 1000 ore, per buone condizioni di raffredda mento e ‘con funzionamento in corrente continua, con temperatura di ambiente che rimanga al disotto di un dato valore come, ad esempio, 40 °C, 70 °C, 125 °C.
Per temperature di ambiente più elevate la potenza dissipabile nei resistori deve essere gradatamente ridotta (derating) ad un valore PDD (derated power) secondo la relazione:
in cui TM è la temperatura d’ambiente massima ammissibile per un dato tipo di resistore, alla quale la potenza dissipata deve essere nulla. Ad esempio, TM≈ 115°C per i resistori a composizione di carbone, a film di carbone e per i resistori a film di cermet (*); TM≈ 130 °C per i resistori a film metallico e per quelli di precisione a filo; T M≈250 °C per i resistori a filo di potenza.
Per il funzionamento a regime impulsivo, con impulsi di durata tp e con periodo di ripetizione tr può essere ammessa una potenza di picco Pp=PD*tr / tp.
In alcuni tipi di resistori si hanno apprezzabili variazioni del valore della resistenza al variare della tensione applicata ai loro terminali. Pur essendo queste variazioni, quando si manifestano, dipendenti in modo assai complesso dalla entità delle variazioni di tensione, in un piccolo intorno della tensione di riferimento V0 è possibile esprimere la dipendenza della resistenza dalla tensione con la relazione:
in cui R0 è il valore della resistenza alla tensione di riferimento, β è il coefficiente di tensione del resistore (β=ΔR/R ΔV), espresso generalmente in %/V o in ppm/V; in generale anche β è funzione sia di R0 che di V0.
Ad esempio, il coefficiente di tensione varia da — 700 ppm/V per i valori più elevati di resistenza dei resistori a composizione di carbone fino a circa 5÷30 ppm/V per i resistori a film di carbone e cermet, e da 10 a 0,05 ppm/V per quelli a film metallico e a film ad ossidi, sebbene in alcuni tipi’ a film spesso il coefficiente di tensione raggiunga valori così elevati come 400 ppm/V.
La tolleranza dei resistori è la deviazione massima del valore della resistenza dal valore nominale, misurata a temperatura di ambiente e a bassa tensione. Viene generalmente espressa in %. Valori tipici comuni di tolleranza sono: 1%, 2 %, 5 % e 10 %; per i resistori di precisione si hanno valori come 0,1 % e 0,01 %, per quelli ad alta precisione.
La potenza dissipabile nelle diverse condizioni di funzionamento definisce, e come conseguenza, la massima tensione che può essere applicata ai capi di un resistore, data dalla relazione:
Tuttavia, per elevati valori della resistenza, in genere si ha una limitazione più restrittiva che deriva dalla rigidità dielettrica dei materiali che costituiscono il resistore, in dipendenza dalle sue dimensioni geometriche. Pertanto la massima tensione nominale che può essere applicata ad un resistore è la massima tensione che esso può sopportare, indipendentemente dalle altre condizioni di funzionamento. Tale tensione è intesa come tensione continua o in valore efficace alla frequenza di rete.
Se la temperatura d’ambiente in cui si trova il resistore è sufficientemente alta da rendere necessario il derating della dissipazione di potenza, anche la tensione dovrà essere ridotta ad un valore che è determinato dalla radice quadrata del rapporto fra la potenza ridotta e la piena potenza nominale.
Nei resistori che funzionano in condizioni ambientali variabili, soprattutto nei riguardi della temperatura e dell'umidità relativa, si manifestano variazioni permanenti (irreversibili) della resistenza. La stabilità nel tempo è la variazione della resistenza sotto condizioni stabilite di uso per 1000 ore, ed è espressa in ±% o ± ppm per 1000 ore.
Il comportamento dei resistori riguardo alla stabilità si giudica sottoponendoli a prove combinate e misurando lo scarto tra il valore iniziale della resistenza e il valore finale al termine delle prove. Il grado di stabilità è misurato, una volta specificate le modalità delle prove, dal rapporto fra questa variazione e il valore iniziale della resistenza.
Il rumore prodotto da un resistore è costituito dal suo rumore termico (Johnson—Nyquist noise) più un rumore dovuto alla corrente applicata. Quest'ultimo dipende dalla forma e costruzione del resistore, mentre il rumore Johnson Nyquist dipende dalla sua resistenza e dalla sua temperatura. In un qualsiasi conduttore l’agitazione termica dovuta alla temperatura produce un movimento caotico degli elettroni liberi che determina piccole fluttuazioni di tensione tra le estremità del conduttore stesso (effetto Johnson) il cui valore medio è nullo. Lo spettro di frequenza di queste fluttuazioni, come è stato dimostrato in base alla teoria statistica della termodinamica e verificato sperimentalmente, è costante fino a frequenze estremamente elevate (dell'ordine di 1014 Hz) e, pertanto, a tutti gli effetti pratici si può considerare che il rumore termico abbia uno spettro uniforme piatto, per cui è anche chiamato rumore bianco.
Il valore quadratico medio della tensione di rumore termico, su una banda di frequenze che va da una frequenza f1 ad una frequenza f2, può essere espresso, per qualunque impedenza che si trova alla temperatura T, dalla relazione:
in cui K è la costante di Boltzmann (K = 1,3806* 1023Joule/°Kelvin); T è la temperatura assoluta dell'impedenza; R (f) è la componente resistiva dell'impedenza, che in generale è funzione della frequenza f. Se la componente resistiva è indipendente dalla frequenza, cioè R(f)=costante=R, la relazione precedente diventa:
con Δf = f2— f1 =larghezza di banda considerata.
Dal punto di vista del rumore un resistore (o una qualsiasi impedenza) può essere considerato come un generatore di tensione di rumore di impedenza interna R e forza elettromotrice efficace data da:
e può essere rappresentato con un generatore equivalente di Thévenin come in fig. 1(a), oppure come un generatore di corrente di rumore come in fig. 1(b), in cui
con G = 1 / R.
Due resistori in serie, di resistenza R1 e R2, rispettivamente alle temperature T1 e T2, possono esser combinati approssimativamente come è mostrato in fig. 1(c) e, analogamente, due resistori in parallelo, di conduttanze G1 e G2, possono essere combinati come è indicato in fig. 1(d). Nei due casi si ha:
in cui:
è la temperatura a cui si deve pensare il resistore equivalente della combinazione dei due resistori in serie o in parallelo.
Per un resistore in cui la temperatura varia lungo la "sua lunghezza, cioè T= T(x) per x che varia da O a 1, [fig. 1(e)], il rumore Johnson-Nyquist viene approssimativamente determinato supponendo il resistore ad una temperatura effettiva di rumore Tn, data dalla relazione:
in cui l è la lunghezza complessiva del resistore.
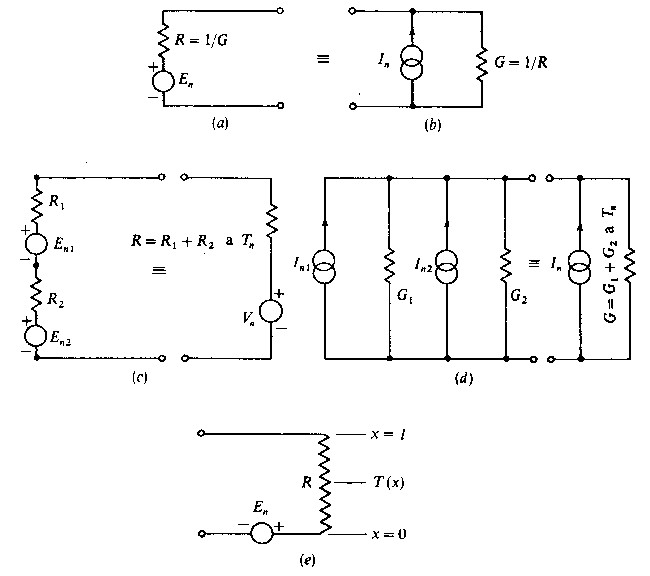
Fig. 1. - Resistore come generatore di rumore. In (a), circuito equivalente di Thévenin con generatore di tensione di rumore; in (b), circuito equivalente di Norton con generatore di corrente di rumore. In (c), rappresentazione equivalente per il rumore di due resistori in serie; in (d), rappresentazione equivalente per il rumore di due resistori in parallelo; in (e) resistore con variazione della temperatura.
Le misure indicano che il rumore Johnson-Nyquist è esattamente osservato nei resistori a filo e a film metallico. I resistori a composizione di carbone e, in minor misura, i resistori a deposito di carbone e cermet, manifestano il rumore di tipo 1 / f, che dipende dalla corrente e varia considerevolmente per entrambi i tipi di resistori e per resistori che sotto altri aspetti sono identici. Il valore quadratico medio della tensione di rumore di tipo 1 / f, per un certo resistore, è proporzionale a log (f2 / f1), in cui f1 e f2 sono le frequenze estreme della banda considerata e la costante di proporzionalità dipende dal valore della resistenza, dalle dimensioni fisiche del resistore e dalla corrente che lo percorre.
Le misure hanno mostrato che per i resistori a composizione di carbone il rumore dovuto alla corrente (current-noise) aumenta linearmente con la corrente fino a circa 15 μA; con correnti più grandi la curva del rumore si approssima ad una parabola.
Per un dato tipo di resistore viene convenzionalmente specificato un indice di rumore (noise index) che è il rapporto fra la tensione efficace di rumore, causata da una specificata corrente attraverso il resistore, e la tensione continua media ai capi del resistore stesso, misurato su una banda di frequenze di una decade, ad una specifica temperatura del resistore. L’unità di misura è microvolt/volt (μV/V), oppure il rapporto viene espresso in decibel (dB) assumendo come riferimento O dB=1 μV/V:
La tensione del rumore di corrente (current-noise) su una banda di frequenze da f1 a f2 è data dalla relazione:
in cui V è la tensione continua ai capi del resistore.
Quando interessa più di una decade di frequenze, le tensioni di rumore di corrente si sommano secondo la radice quadrata del numero delle decadi. La banda da 10 Hz a 100 kHz ha, quindi, un rumore di valore efficace doppio di quello della banda da 1O a 100 Hz (una decade), cioè quattro decadi (10 Hz +100 kHz) hanno il doppio del rumore di una decade.
I resistori a filo, tranne che per le possibili terminazioni «rumorose» e per le imperfezioni del filo, producono soltanto l’inevitabile rumore termico. I resistori a film metallico hanno indici di rumore circa da - 30 a - 40 dB, con rumore più basso in corrispondenza dei valori più bassi della resistenza. I resistori a film di carbone hanno indici da circa + 10 dB fino a - 30 dB. I resistori a composizione di carbone hanno indici da circa + 40 dB per i valori più elevati di resistenza dei tipi da 1 / 10 di watt fino a un massimo di circa O dB per i valori più bassi dei tipi da 2 W. e
Naturalmente la tensione di rumore totale è la somma di quella del rumore termico Johnson-Nyquist e di quella del rumore di corrente.
Comportamento alle alte frequenze
Persino a frequenze dell'ordine di qualche MHz non è più possibile, nemmeno in prima approssimazione, considerare i resistori costituiti da una resistenza pura, ma è necessario, al fine di determinareil comportamento alle frequenze elevate, rappresentare il resistore con un circuito equivalente in cui si tenga conto della resistenza effettiva, della induttanza propria dell'elemento resistivo e dei terminali, della capacità diretta fra i terminali e della capacità distribuita, considerando che questi elementi, particolarmente la resistenza effettiva e la capacità distribuita, variano al variare della frequenza. Nel determinare il comportamento in frequenza non soltanto interviene la natura dell'elemento resistivo vero e proprio, ma anche il tipo di supporto e di rivestimento, le dimensioni geometriche del corpo del resistore, la forma e le dimensioni dei terminali.
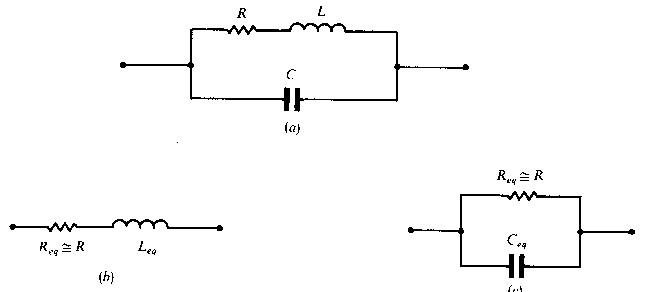
Fig 2 - circuiti equivalenti per un resistore
Un resistore può essere rappresentato con un circuito equivalente come quello in fig. 2(a), in grado di rappresentare con sufficiente approssimazione il resistore stesso fino a frequenze non molto elevate. R è la resistenza serie dell'elemento. Nei resistori a film di valore al disopra di 50 ohm, R è essenzialmente indipendente dalla frequenza fino a frequenze nella regione dei GHZ. Nei valori molto bassi di resistenza, se non mascherato da altre variazioni, l'effetto pelle nei fili dei terminali potrebbe essere percettibile se i terminali sono lunghi e se sono di materiale magnetico. L’effetto pelle produce anche variazioni di R nei resistori a filo poiché la distribuzione della densità di corrente sulla sezione del conduttore non è più uniforme. In pratica, tuttavia, l’effetto pelle sembra essere di minore importanza per i resistori di tipo convenzionale e il comportamento è dominato da altre caratteristiche. Si può, pertanto, assumere il valore di R costante con la frequenza. La capacità può variare leggermente, poiché le costanti dielettriche variano con la frequenza e con la tensione, ma questo effetto può essere ignorato nell’analisi del circuito di fig. 2(a). L’impedenza di questo circuito, che è quella vista ai terminali del resistore, è data dall’espressione:
Il campo di frequenze di corretta utilizzazione del resistore sarà quello per cui si verificano le condizioni:ωL << R, 1 / ωC >> R, cioe: ω2LC << 1, ωRC << 1, e quindi la precedente espressione può essere approssimata con la seguente:
L’impedenza Z fra i terminali del resistore si può, quindi, ritenere costituita da una resistenza equivalente Req ≈ R in serie con una reattanza equivalente Xeq data da:
Se L > R2C la reattanza è induttiva e il circuito equivalente di fig. 2(a) si riduce a quello di fig. 2(b) con Leq = L - R2C. Se invece risulta L < R2C la reattanza è negativa, cioè capacitiva, e si può constatare che il circuito di fig. 2(a) può essere sostituito con quello di fig. 2(c) in cui Ceq=(R2C - L) / R2.
La quantità
è la costante di tempo del resistore, uguale a Leq/Req oppure a ReqCeq, nei limiti delle approssimazioni fatte, e costituisce un indice di qualità del resistore nei riguardi degli effetti degli elementi reattivi parassiti. Un analogo indice di qualità è dato dall’angolo di fase (p del resistore, cioè dall'argomento dell'impedenza Z sopra calcolata; si ha:
Il circuito equivalente di fig. 2(a) rappresenta una prima approssimazione di un resistore per determinare il suo comportamento con la frequenza. Una migliore approssimazione per un resistore di forma tubolare si ottiene considerando il resistore suddiviso in diverse sezioni, con ciascuna sezione avente un circuito equivalente analogo a quello di fig. 2(a).
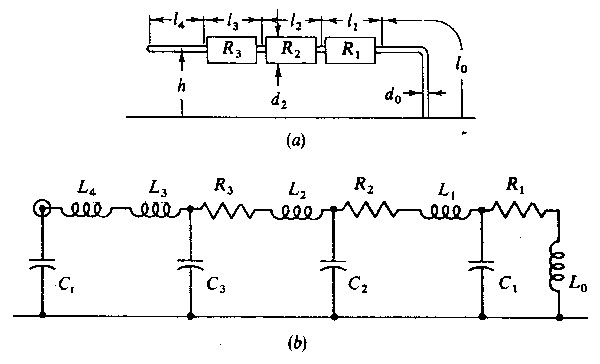
Fig 3 - Approsimazione a più sezioni di un resistore tubolare orizzontale; in (a) approsimazione a tre sezioni; in (b) Circuito equivalente
In fig. 3 e mostrata un’approssimazione a tre sezioni di un resistore tubolare montato orizzontalmente e il corrispondente circuito equivalente. Per n sezioni identiche, le grandezze caratteristiche di ciascuna sezione sono:
in cui ε0 e μ0 sono, rispettivamente, la costante dielettrica e la permeabilità magnetica del vuoto; L0 e Ln+1 in fig. 3 sono le induttanze corrispondenti alle induttanze dei terminali del resistore; C, è la capacità concentrata associata con il terminale. Nelle espressioni sopra riportate le dimensioni sono espresse in metri, Ci in farad e Li in henry.
Un resistore per essere adatto per il funzionamento alle alte frequenze dovrà soddisfare i seguenti requisiti generali: le sue dimensioni dovranno essere le più piccole possibili, dovrà avere un basso valore di resistenza; dovrà essere del tipo a film; tutte le connessioni al resistore dovranno essere le più corte possibili; non vi dovrà essere alcuna improvvisa discontinuità geometrica lungo la sua lunghezza. Un resistore lungo e sottile ha una caratteristica di frequenza migliore di uno corto e grosso.