Funzione Derivata

Dettagli

Categoria: Elettronica

Pubblicato Domenica, 03 Novembre 2013 09:52

Scritto da Super User

Visite: 53372

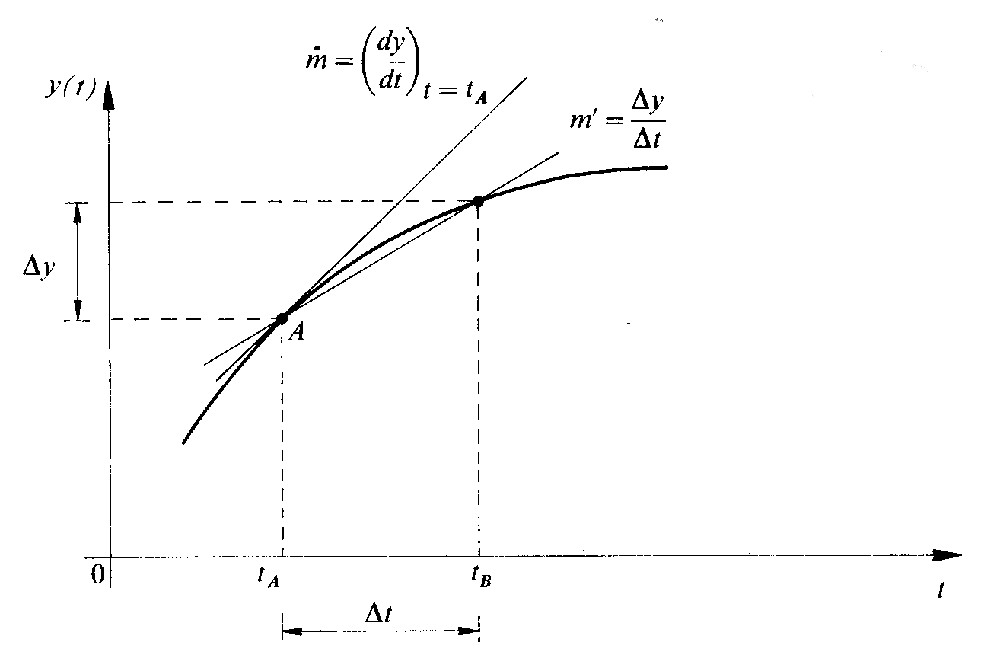
Fig 1.1 - Derivata in un punto come coefficiente angolare della tangente nel punto A.

In fig. 1.1 è rappresentata una generica funzione del tempo y(t). In numerosi fenomeni fisici, come quelli relativi ai circuiti induttivi e capacitivi, non interessa tanto la funzione in sé, quanto piuttosto la sua rapidità di variazione nel tempo.

In fig. 1.1, nell'intervallo di tempo Δt la funzione subisce un incremento Δy. Il rapporto:

rappresenta il coefficiente angolare della retta secante la curva nei punti A e B.

Avvicinando il punto B ad A, l’intervallo A: si riduce progressivamente e la secante si avvicina sempre più alla tangente nel punto A; anche il rapporto

si approssima sempre più al coefficiente angolare m della tangente. La derivata in un punto è proprio il coefficiente angolare della tangente la curva nello stesso punto:

Commentiamo i vari simboli usati in questa espressione. La derivata è rappresentata dal rapporto,

nel quale la lettera d sostituisce il Δ usato in precedenza; questo significa che si considerano intervalli di tempo cosi piccoli da far coincidere la retta secante con la tangente.

L’indicazione t = t _A, scritta ai piedi della parentesi, è necessaria per precisare l'istante di tempo nel quale viene calcolata la derivata.

Infatti, nei diversi punti della funzione y(t), la derivata assume valori diversi: anch'essa è dunque una funzione del tempo, e può essere messa in diagramma. Nell'esempio di fig. 1.2 è rappresentata una generica funzione y(t), sotto la quale è tracciata la funzione derivata, ottenuta riportando, punto per punto, il valore del coefficiente angolare corrispondente.

All'istante t₁ la funzione presenta la massima velocità di salita: la derivata nello stesso istante assume il massimo valore positivo. All'istante t₂ la tangente è orizzontale (m₂ = 0): la funzione derivata passa per lo zero.

Negli intervalli in cui la funzione y(t) è crescente la sua derivata è positiva; dove y(t) è decrescente la derivata risulta negativa. Nei punti di massimo e minimo, dove la tangente è orizzontale, la derivata è nulla.

Risulta evidente che la derivata di una retta è costante al variare del tempo, e coincide con il coefficiente angolare della retta stessa.

Fenomeni statici, rappresentati da una retta orizzontale, presentano derivata nulla in tutti i punti, coerentemente con il fatto che non manifestano variazioni nel tempo.

• < Prec
• Succ >