Trasformatore ideale in regime sinusoidale
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Sabato, 27 Settembre 2014 10:32
- Scritto da Super User
- Visite: 21721
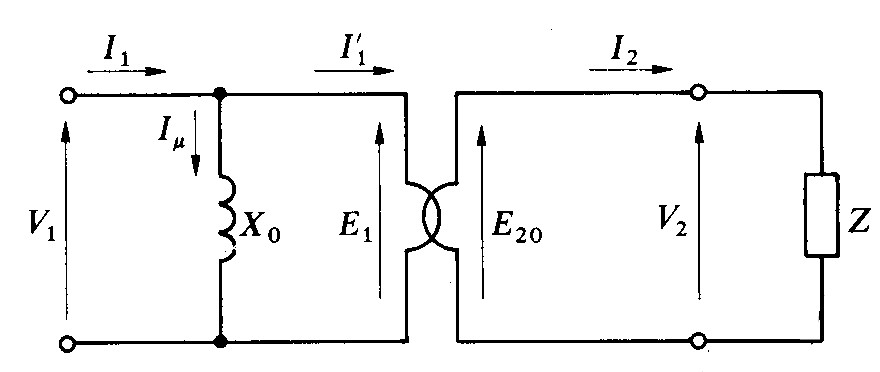
Fig. 2.1 - Circuito equivalente del trasformatore in regime sinusoidale sotto carico che considera solo la corrente magnetizzante.
Il circuito equivalente, ricavato nell'articolo «Trasformatore ideale sotto carico», può essere utilizzato per qualunque forma d'onda della tensione primaria.
Tuttavia una particolare attenzione va dedicata al comportamento del trasformatore in regime sinusoidale, poiché il suo utilizzo principale è rivolto alla trasformazione della potenza industriale, che è appunto distribuita utilizzando grandezze di forma sinusoidale.
Consideriamo in prima approssimazione un trasformatore senza perdite, sia nel rame sia nel ferro, e senza flusso disperso, alimentato con la tensione sinusoidale
Il circuito equivalente si presenta come in fig. 2.1 ed è del tutto simile a quello visto nell'articolo «Trasformatore reale» di fig. 1.11, dove in corrispondenza dell'induttanza L0 si è posta la reattanza
Si vuole determinare il valore e la forma d'onda del flusso magnetico.
Come è noto dall'articolo «Trasformatore monofase ideale» il valore e la forma d'onda del flusso sono imposti dalla tensione applicata al primario. Con il circuito equivalente di fig. 2.1 nel quale la resistenza e la reattanza di dispersione primarie sono nulle, in ogni istante la tensione e1 risulta identica a v1
In accordo con quanto esposto nell'articolo «Trasformatore monofase ideale», ricordiamo che il flusso deve avere valore e forma tali da soddisfare l'equazione
Esprimendoci in termini matematici, la tensione è la derivata del flusso e considerando la formula inversa
ricaviamo
Il flusso è dunque l'integrale della tensione, qualunque sia la forma d'onda.
Nel caso presente stiamo considerando una tensione primaria sinusoidale e dobbiamo dedicare un pò di attenzione a questa forma d'onda.
In fig. 2.2a è tracciata la tensione
L'integrale di una funzione sinusoidale è la funzione cosinusoidale negativa rappresentata in fig. 2.2b
Dalla trigonometria è noto che
Possiamo quindi scrivere
Il flusso ha un andamento sinusoidale simile a quello della tensione, ma sfasato di 90° in ritardo.
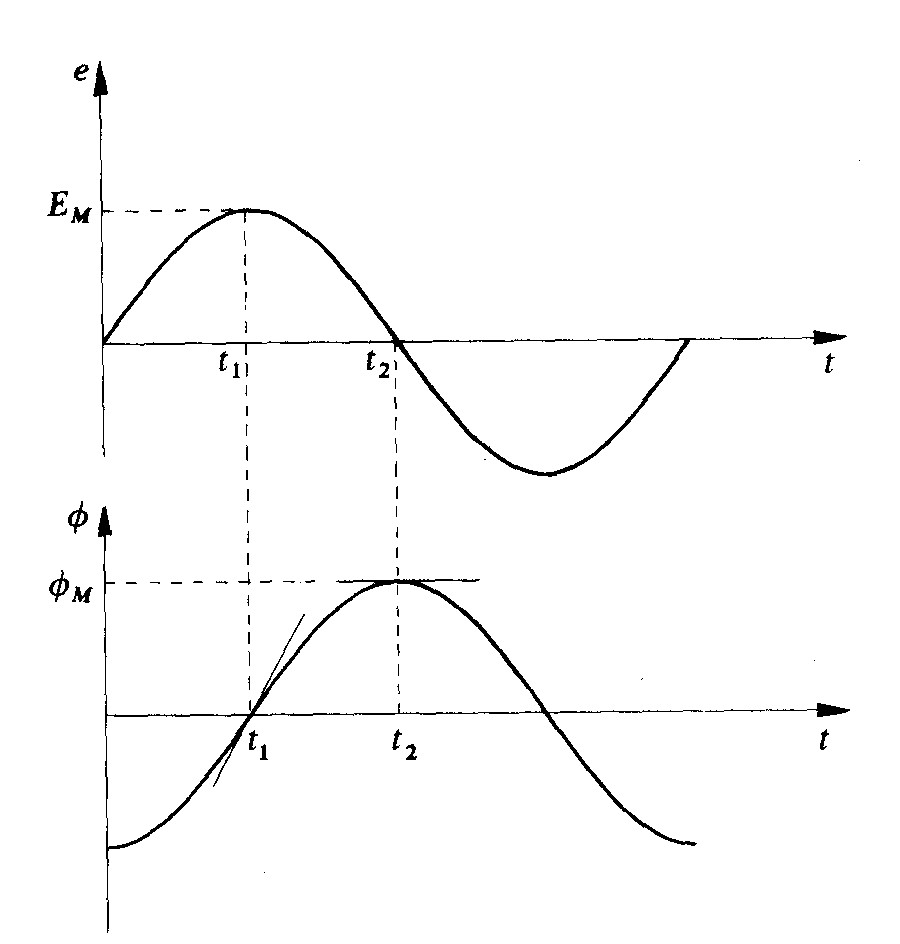
Fig. 2.2 - Relazione tra tensione e flusso magnetico in regime sinusoidale. Osservare che quando il flusso passa per lo zero (t1) la sua derivata è massima: in corrispondenza si ha la massima tensione.
Dalla fig. 2.2 rileviamo che nell'istante t2 il flusso raggiunge il valore massimo, ma con derivata nulla (la sua tangente geometrica è orizzontale): la tensione passa per lo zero.
Nell'istante t1 il flusso ha valore nullo ma ha derivata massima (è massima l'inclinazione della tangente): la tensione presenta qui il suo valore massimo EM. Risolto il problema di determinare la forma d’onda del flusso, rimane ora da calcolare il valore di ΦM.
Questo problema è di immediata soluzione, ricordando la formula fondamentale del flusso esposta all'articolo «Trasformatore monofase ideale»
Tale relazione è valida per qualsiasi forma d'onda e quindi anche per la sinusoidale.
Del flusso interessa sempre calcolare il valore massimo, poiché su questo viene dimensionata la sezione del circuito magnetico. Al contrario la tensione viene solitamente indicata attraverso il valore efficace E.
Modifichiamo la formula fondamentale in modo da poter calcolare ΦM in funzione di E anziché di EM. Utilizzando il fattore di forma Kf e ricordando che
si ricava
Per la sinusoide il valore di Kf risulta
- Prec
- Succ >>