Elettrotecnica
Rifasamento
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Lunedì, 11 Agosto 2014 06:09
- Scritto da Super User
- Visite: 10977
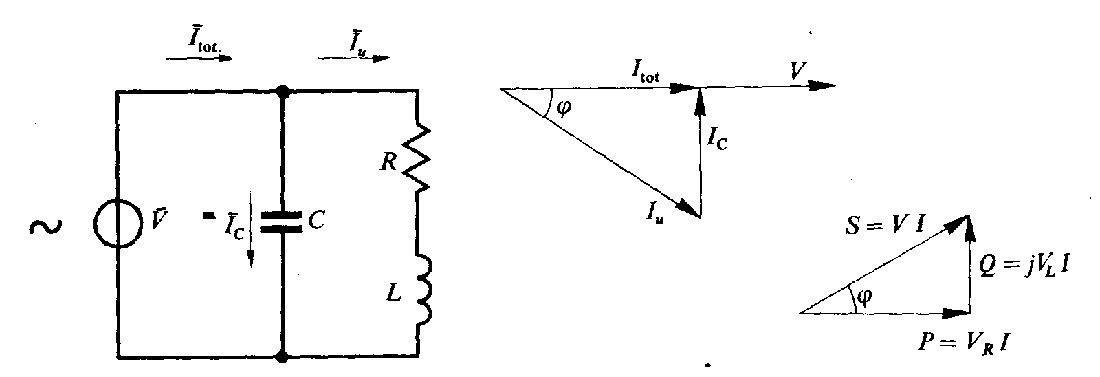
Fig. 4.9 - Rifasamento di un carico ohmico-induttivo per mezzo di un condensatore.
La potenza attiva rappresenta l’energia che, in un intervallo di tempo, viene effettivamente trasferita dal generatore all'utilizzatore e trasformata in qualche altra forma. Per la sua produzione è necessario ricorrere ad una fonte di energia primaria (ad esempio combustibili, salti idraulici, ecc.). Anche le tariffe dell'energia elettrica sono basate sulla misura del'energia attiva.
Circuito ohmico-induttivo
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Sabato, 09 Agosto 2014 09:34
- Scritto da Super User
- Visite: 13746
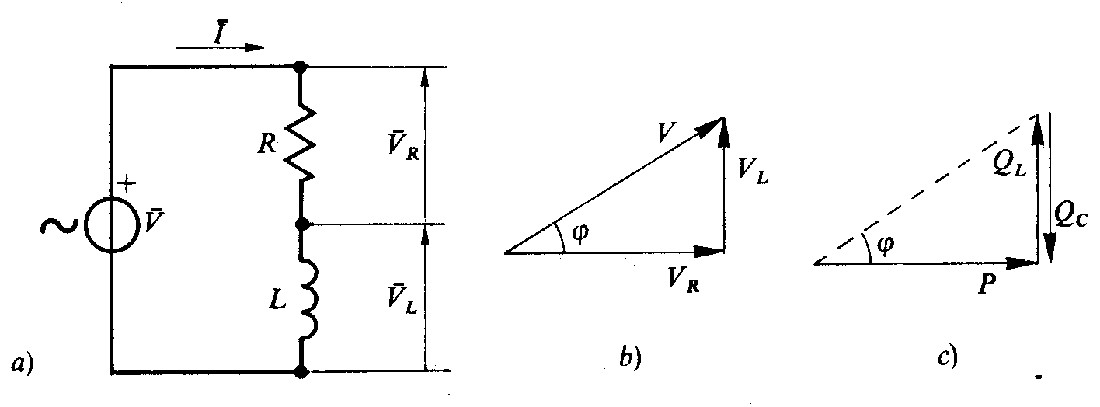
Fig. 4.6 - Triangolo delle tensioni e delle potenze in un circuito R-L.
Ci proponiamo di calcolare le potenze che interessano il circuito di fig. 4.6 nel quale un generatore di tensione v = Vmax, sen(ωt) alimenta un circuito serie ohmico-induttivo.
La tensione ai capi di R sarà VR, quella ai capi di L sarà VL e la loro somma vettoriale corrisponde a V (fig. 4.6 b). Dall'articolo «Potenza in regime sinusoidale» è noto che la resistenza assorbe la potenza attiva P = VR * I, mentre la reattanza è interessata dalla potenza reattiva Q = VL*I.
Potenza in regime sinusoidale
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Giovedì, 07 Agosto 2014 05:40
- Scritto da Super User
- Visite: 7025
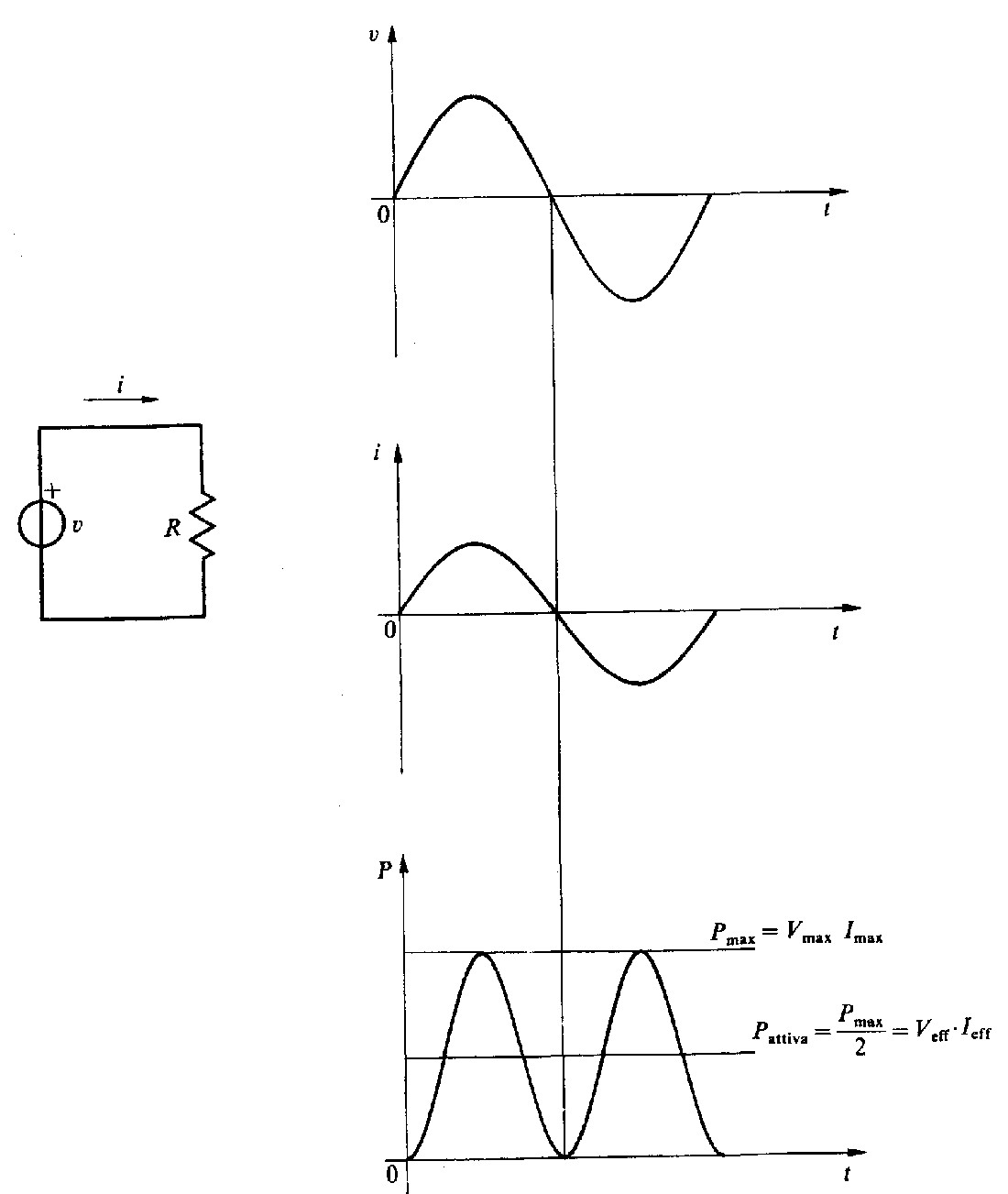
Fig. 4.4 - Potenza attiva in regime sinusoidale.
Consideriamo il circuito di fig. 4.4, nel quale un resistere è alimentato da un generatore di tensione sinusoidale. Le espressioni della tensione e della corrente sono
Potenza in regime variabile
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Mercoledì, 06 Agosto 2014 05:38
- Scritto da Super User
- Visite: 4383
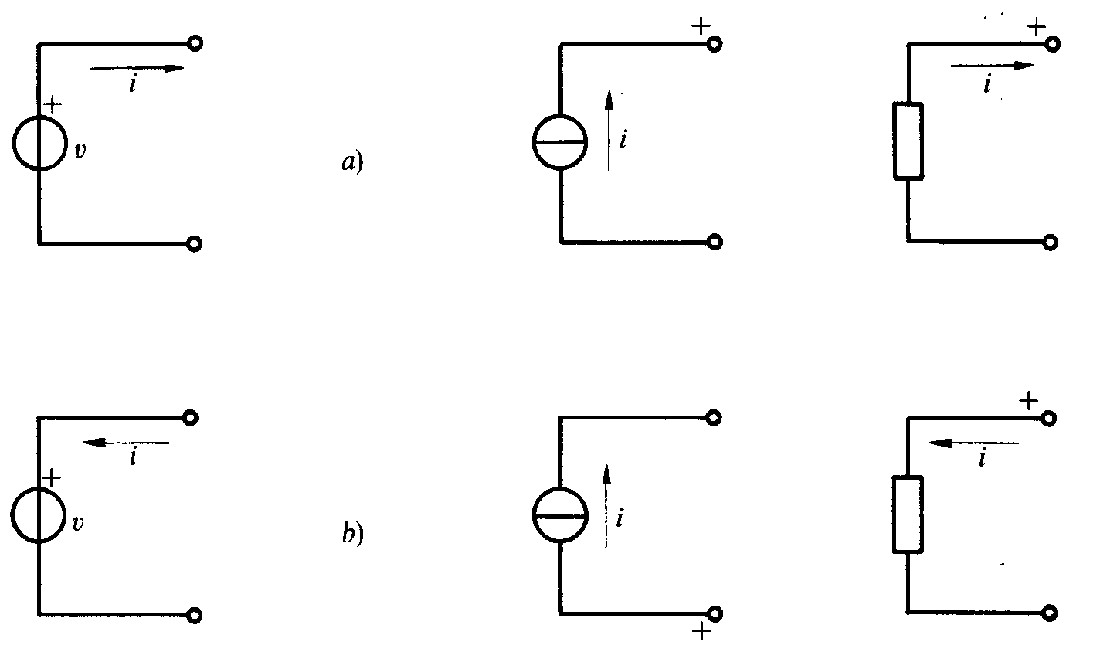
Fig. 4.1 - a) potenza generata; b) potenza assorbita.
Come già esposto nei primi articoli, la potenza è definita come prodotto tra la tensione e la corrente e in un bipolo può essere generata o assorbita; è generata quando la corrente esce dal morsetto positivo, assorbita nel caso opposto (fig. 4.1). Nel caso in cui sia la tensione che la corrente variano nel tempo, anche la potenza diventa funzione del tempo e può quindi essere rappresentata in un diagramma.
Circuito R-L in serie
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Domenica, 03 Agosto 2014 08:16
- Scritto da Super User
- Visite: 8591
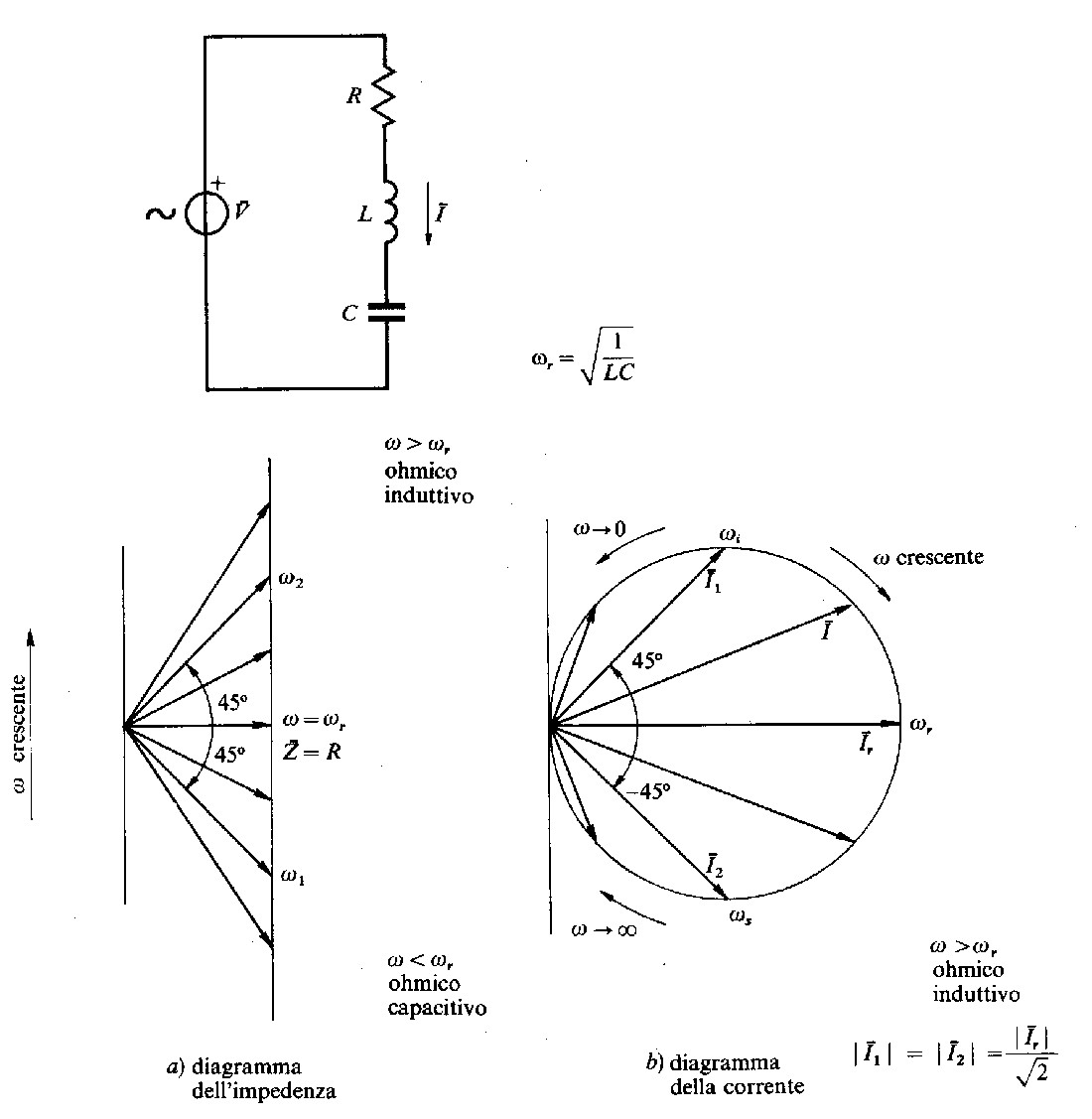
Fig. 3.5 - Risposta al variare della pulsazione del circuito R-L-C- serie.
Per descrivere la risposta in frequenza del circuito R-L-C in serie di fig. 3.5 si segue la stessa procedura adottata per i circuiti R-L ed R-C.
Filtri
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Giovedì, 31 Luglio 2014 05:40
- Scritto da Super User
- Visite: 5220

Fig. 3.1 - Risposta al variare della pulsazione di un circuito R-L; a) circuito; b) diagramma dell'impedenza al variare di ω; c) diagramma delle tensioni; d) diagramma della corrente.
Il circuito di figura 3.1 esiste un valore di pulsazione che indichiamo con ωt, tale che
Risposta in frequenza dei circuit in C.A.
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Lunedì, 28 Luglio 2014 10:19
- Scritto da Super User
- Visite: 4220

Fig. 3.1 - Risposta al variare della pulsazione di un circuito R-L; a) circuito; b) diagramma dell'impedenza al variare di ω; c) diagramma delle tensioni; d) diagramma della corrente.
Impedenza equivalente
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Venerdì, 04 Luglio 2014 07:44
- Scritto da Super User
- Visite: 24074
Le impedenze, come tutti gli altri bipoli, possono essere collegate nei modi più svariati, a formare reti complesse.
Consideriamo i due casi, particolarmente ricorrenti, del collegamento di impedenze in serie ed in parallelo.
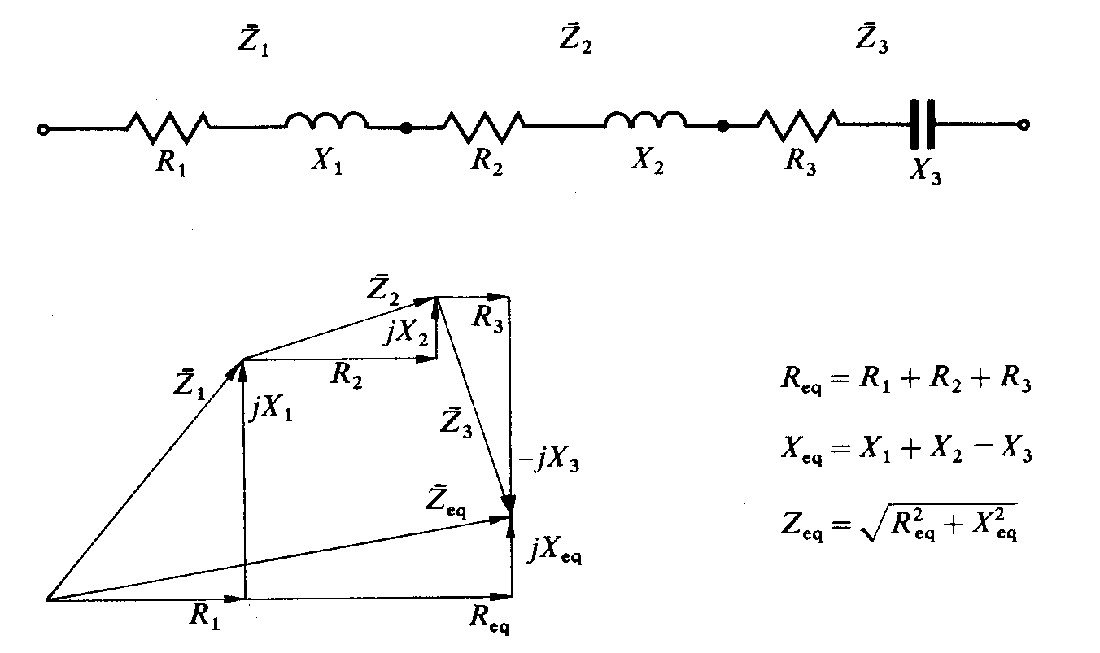
Fig. 2.9 - Impedenza equivalente a più impedenze in serie.
Circuito R-L in serie - Impedenza Complessa
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Sabato, 21 Giugno 2014 09:10
- Scritto da Super User
- Visite: 10240
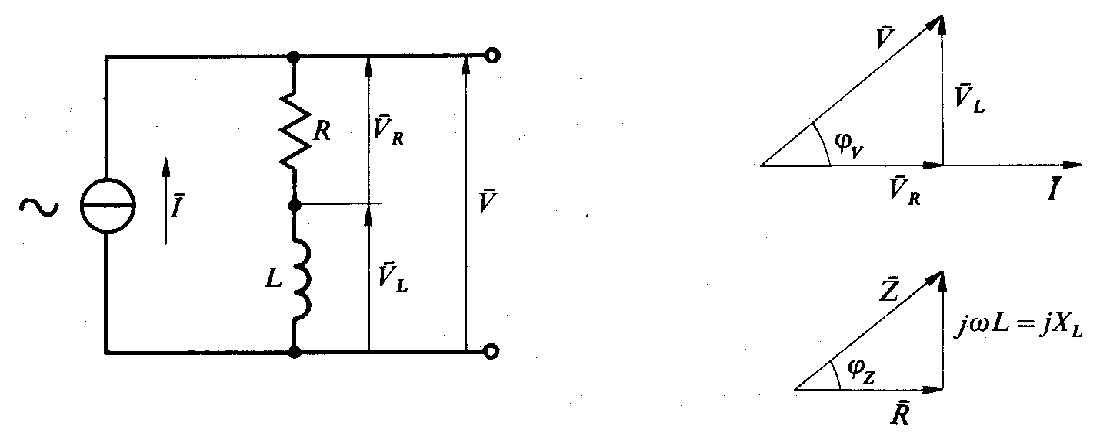
Fig. 2.5 - Impedenza ohmico-induttiva.
Negli articoli precedenti sono stati considerati separatamente gli elementi R, L, C. In pratica tali elementi si trovano spesso combinati e dobbiamo perciò trattare configurazioni più complesse.
Circuito resistivo in regime sinusoidale
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Lunedì, 02 Giugno 2014 12:20
- Scritto da Super User
- Visite: 5263
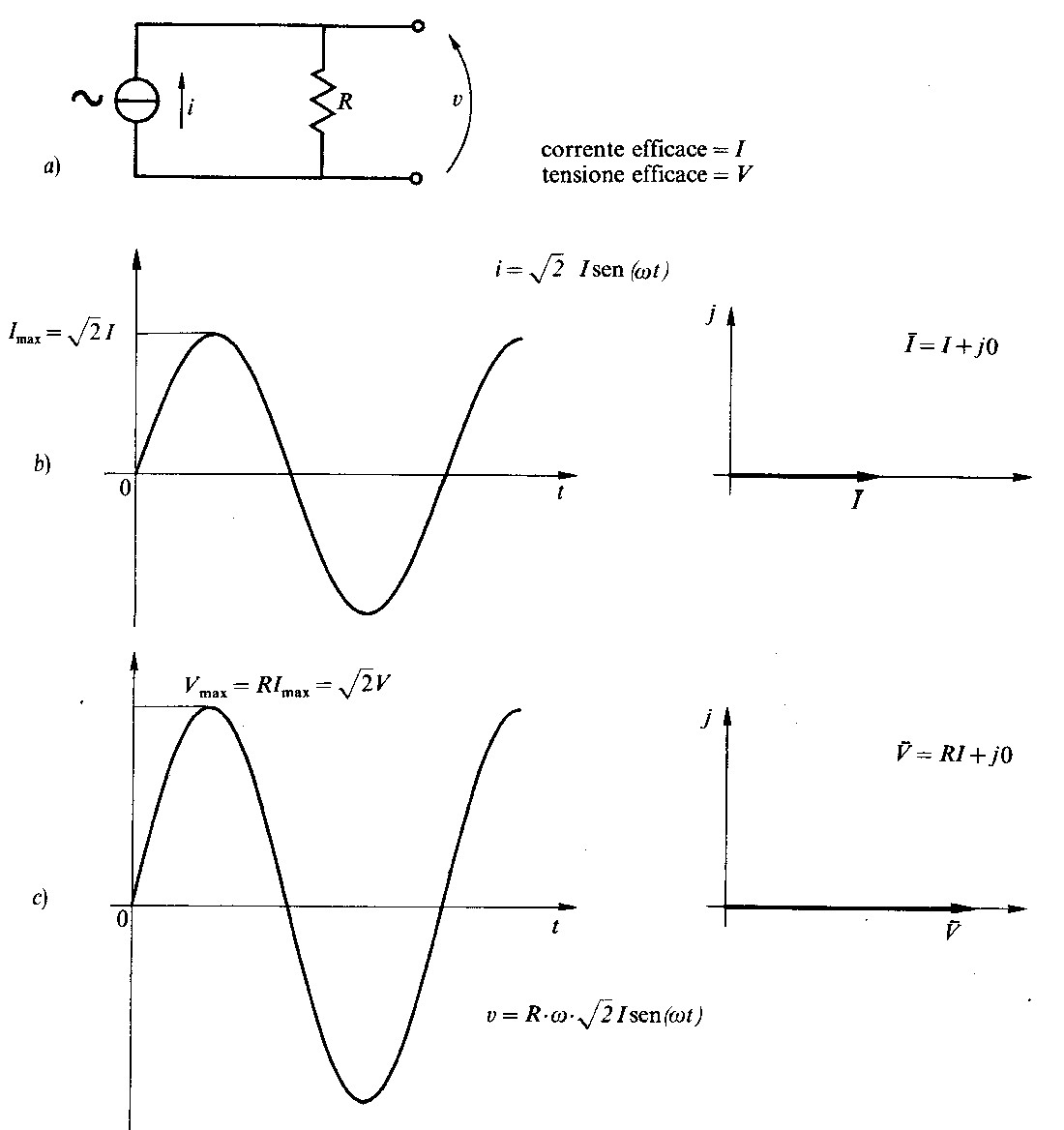
Fig 2.1 - Tensione e corrente ai capi di un resistore in regime sinusoidale nelle rappresentazioni analitica, sinusoidale, vettoriale e simbolica.
Un resistere è alimentato da un generatore di corrente sinusoidale di valore efficace I e pulsazione ω (fig. 2.1). Accanto al simbolo del generatore è indicato il senso positivo della corrente, nonostante questa sia alternata; l’indicazione è necessaria per stabilire univocamente il morsetto di riferimento per la determinazione della fase. Poiché nel circuito è presente un solo generatore è comodo assumerlo come riferimento attribuendogli fase nulla.
Circuito risonanza in parallelo
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Domenica, 13 Luglio 2014 09:46
- Scritto da Super User
- Visite: 9382
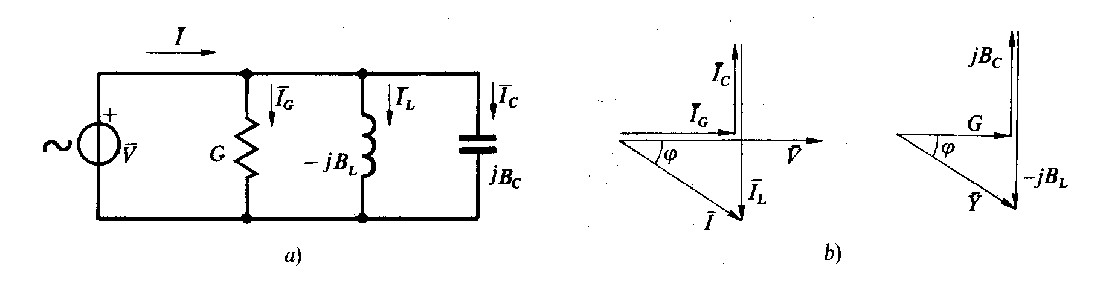
Fig. 2.13 - Cirbuito G-L-C in parallelo e relativi diagrammi.
Il circuito di fig. 2.13 a) è costituito da un resistere, un induttore ed un condensatore collegati in parallelo ed alimentati da un generatore di tensione. Con questa disposizione risulta conveniente far uso dell'ammettenza anziché dell'impedenza; il diagramma delle correnti è rappresentato in fig. 2.13 b). La corrente risultante è data da
Circuito R-L-C - Risonanza
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Giovedì, 26 Giugno 2014 16:37
- Scritto da Super User
- Visite: 305272
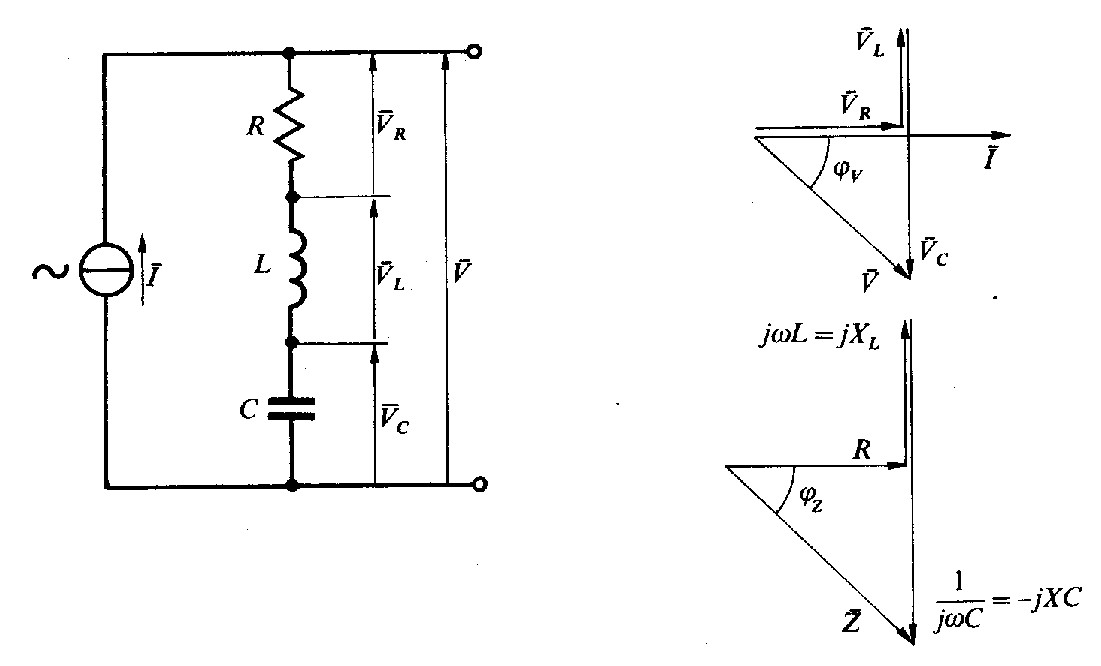
Fig. 2.7 - Circuito R-L-C: diagramma vettoriale della tensione e dell'impedenza.
Nel circuito di fig. 2.7 dobbiamo calcolare l’impedenza vista dai morsetti del generatore. La tensione V è data dalla somma vettoriale
Circuito puramente capacitivo
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Lunedì, 16 Giugno 2014 18:02
- Scritto da Super User
- Visite: 6907
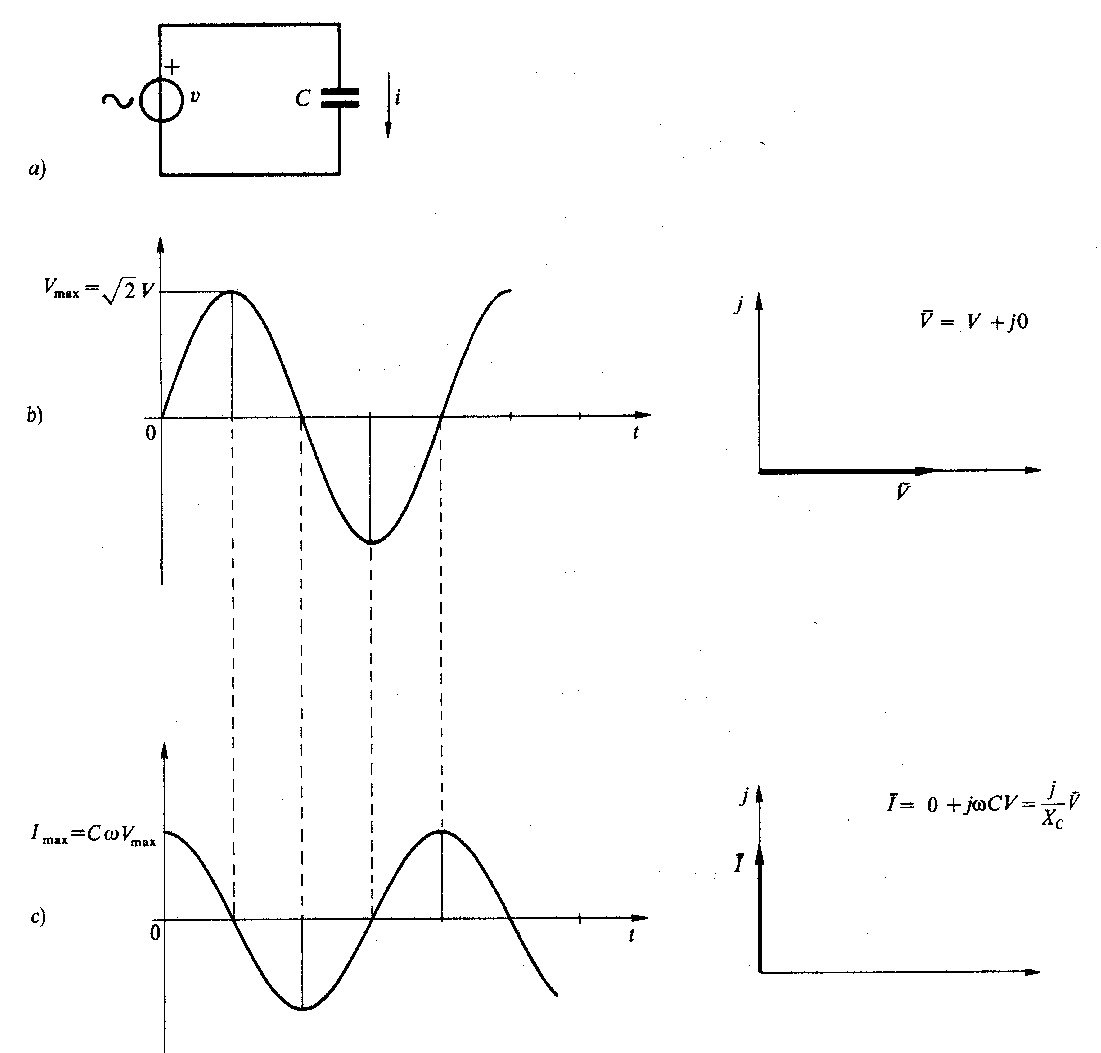
Fig 2.4 - Tensione e corrente ai capi di un condensatore in regime sinusoidale
Un condensatore ideale è collegato ad un generatore di tensione sinusoidale,come nel circuito di fig. 2.4. Assumendo fase uguale a zero, l'espressione della tensione istantanea è
Operazioni lineari sui numeri complessi
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Domenica, 18 Maggio 2014 07:55
- Scritto da Super User
- Visite: 4875
Ridefiniamo sui numeri complessi le stesse operazioni già viste sulle sinusoidi e sui vettori. La somma o la differenza di due o più numeri complessi è un numero complesso avente la parte reale uguale alla somma o differenza delle parti reali e la parte immaginaria uguale alla somma o differenza di tutte le parti immaginarie
Circuiti R-L ed R-C in parallelo - Ammettenza
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Domenica, 13 Luglio 2014 08:30
- Scritto da Super User
- Visite: 16499
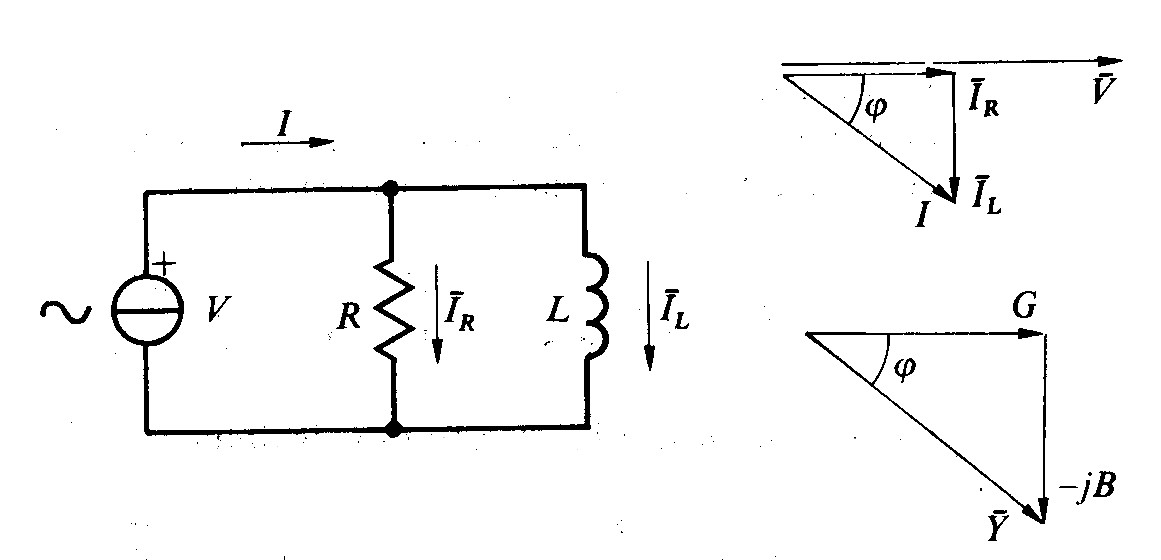
Fig 2.11 - Circuito R-L parallelo:diagramma delle correnti e dell'ammettenza
Se si collegano due elementi ideali in parallelo, come ad esempio il resistere e l’induttore di fig. 2.11 e si alimenta il circuito con un generatore di tensione, la corrente in ogni ramo risulta
Circuito R-C in serie
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Lunedì, 23 Giugno 2014 12:57
- Scritto da Super User
- Visite: 5450
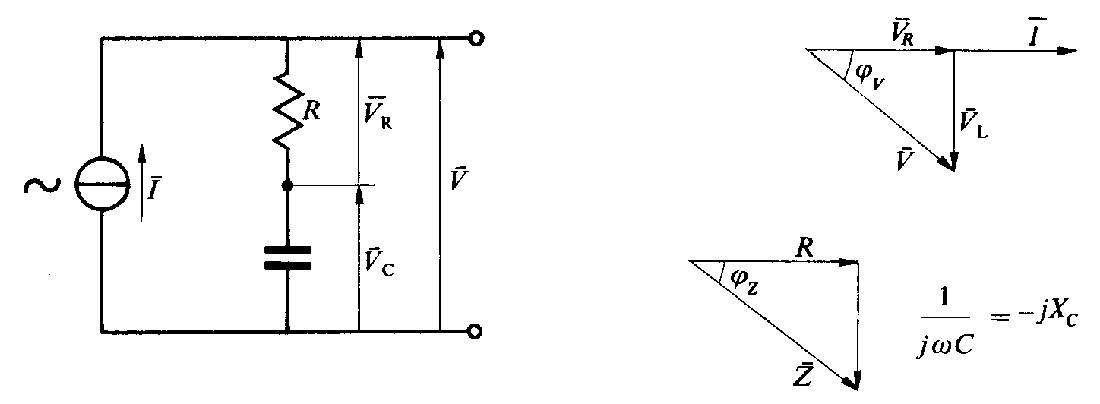
Fig. 2.6 - Impedenza ohmico-capacitiva.
Se il circuito esaminato è quello di fig. 2.6, nel quale sono collegate in serie una resistenza ed una capacità, procedendo analogamente all'articolo «Circuito R-L in serie» si ottiene:
Circuito puramente induttivo
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Giovedì, 05 Giugno 2014 16:18
- Scritto da Super User
- Visite: 12460
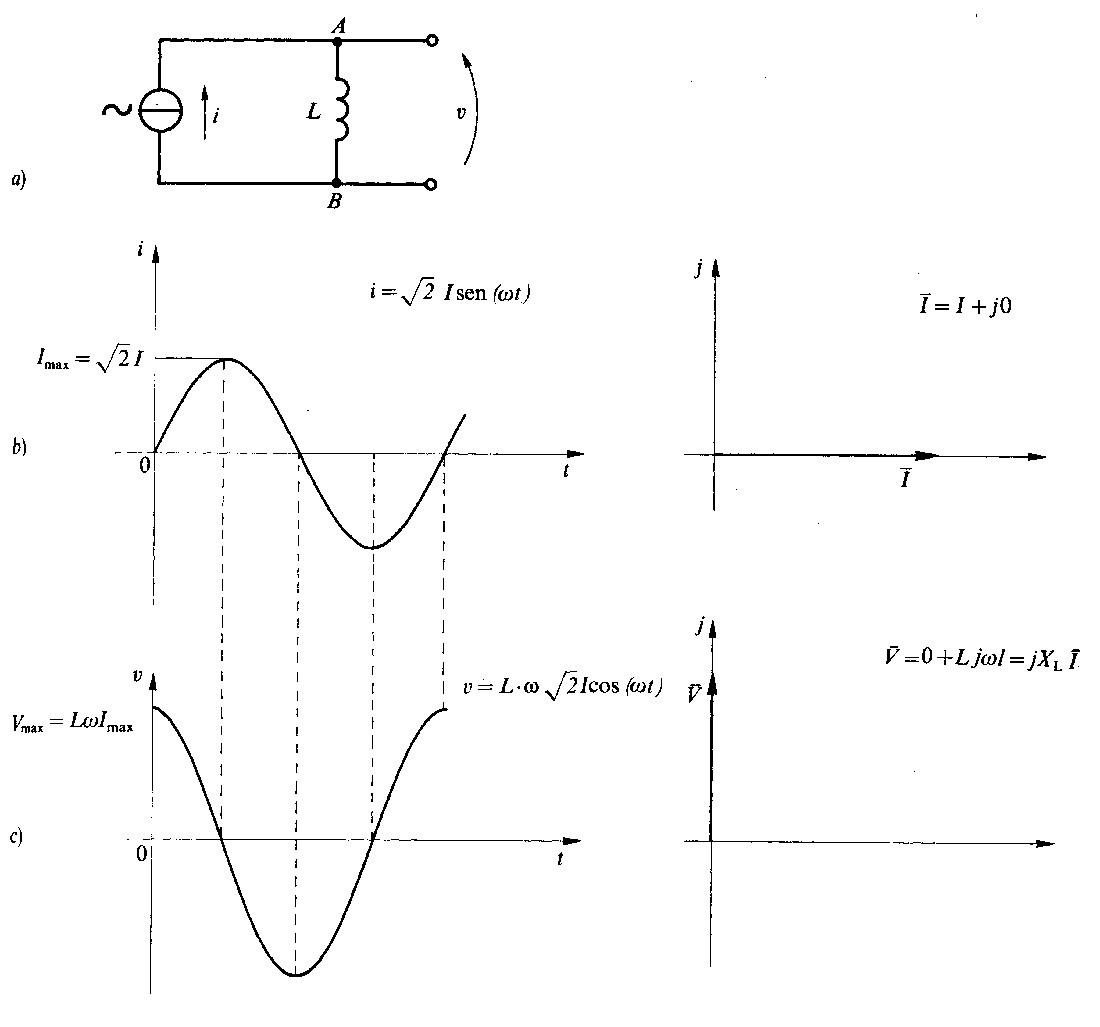
Fig 2.2 - Corrente e tensione ai capi di un induttore in regime sinusoidale
Consideriamo un induttore ideale avente resistenza nulla e caratteristica magnetica lineare (ottenibile ad esempio per mezzo di una bobina in aria od avvolta su un circuito magnetico avente un ampio traferro).
Numeri complessi
- Dettagli
- Categoria: Elettrotecnica
- Pubblicato Venerdì, 16 Maggio 2014 05:35
- Scritto da Super User
- Visite: 6439
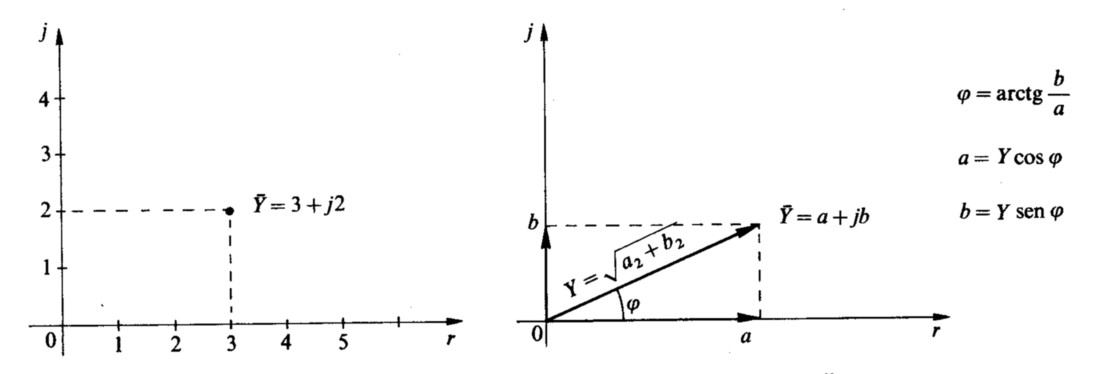
Fig 1.21 - A) Rappresentazione di un numero complesso sul piano di Gauss. B) Rappresentazione di un vettore sul piano di Gauss a componente reale b componente immaginaria
I vettori, oltre che graficamente, possono essere trattati analiticamente utilizzando la perfetta corrispondenza con i numeri complessi, composti dalla somma di un numero reale e di un numero immaginario. La rappresentazione dei vettori per mezzo dei numeri complessi è detta rappresentazione simbolica.Indicando con Y un generico numero complesso, poniamo
Altri articoli...
- Rappresentazione vettoriale delle sinusoidi
- Operazioni lineari sulle sinusoidi
- Fase di una sinusoide
- Funzione sinusoidale
- Fattore di forma
- Valore Efficace
- Funzione Periodica
- Circuiti di spegnimento
- Apertura di un circuito induttivo
- Transitori nei circuiti R - L
- Forza di attrazione di un elettromagnete
- Correnti parassite
- Perdite per isteresi
- Energia nei circuiti magnetici
- Caratteristica dei circuiti magnetici in parallelo
- Caratteristica dei circuiti magnetici in serie
- Calcolo dei circuiti magnetici
- Diversi tipi di materiali magnetici
- Caratteristica di magnetizzazione
- Materiali ferromagnetici